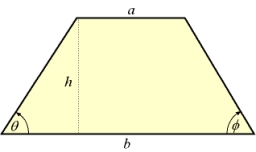
Trapezoid height angle
In the isosceles trapezoid ABCD, its bases AB = 20cm, CD = 12cm and arms AD = BC = 8cm are given. Specify its height and alpha angle at vertex A
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Base RR odd
 The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm.
The base of the prism is an isosceles trapezoid ABCD with bases AB = 12 cm, and CD = 9 cm. The angle at vertex B is 48° 10'. Determine the volume and area of the prism if its height is 35 cm. - Trapezoid Perimeter Pythagorean
 The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Trapezoid angle calculation
 In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle.
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Triangle ABP
 An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP.
An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP. - Trapezoid angles
 Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Trapezoidal prism
 Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Trapezoid proof
 Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid.
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid.
