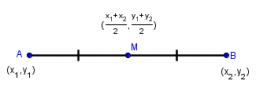
Line construction
Draw line AB if you know one of its extreme points and the center of line S.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
statisticsgeometrythemes, topicsGrade of the word problem
Related math problems and questions:
- Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Point distance
Draw the line segment AB, AB = 5 cm. Draw a set of points 2 cm away from line AB. What is the district's department? - Circle construction
Draw the line KL = 55mm. Draw a circle k with center K and a radius of 4cm. Mark the points to belong to the circle and connect them with point L. - Square
Draw a square on the edge of a = 4 cm. Mark the center of symmetry S and all axes of symmetry. How many axes of symmetry do you have? Write down. - Sphere equation
Obtain the equation of a sphere. Its center is on the line 3x+2z=0=4x-5y and passes through the points (0,-2,-4) and (2,-1,1). - Rhombus construct
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Trisection of a line segment
Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles).
