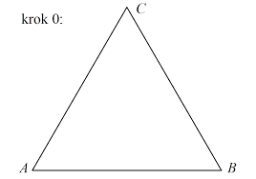
Trisection of a line segment
Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles).
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Distance of the parallels
Find the distance of the parallels, which equations are: x = 3-4t, y = 2 + t and x = -4t, y = 1 + t (instructions: select a point on one line and find its distance from the other line) - Ratio of triangles areas
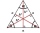In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Trapezoid thirds
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - Trapezoid - construction
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Triangle construction sides
Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm - Katy MO
Kate drew a triangle ABC. The middle of the line segment AB is marked as X, and the center of the side AC is marked as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximall
