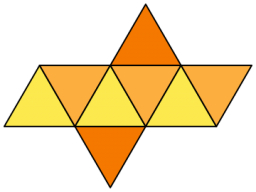
Octahedron in a cube
What largest octahedron can we place inside a cubical box with sides equal to 72?
Correct answer:
Tips for related online calculators
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Ribbon on the cube
A cubical gift box is tied with a piece of ribbon. If the total length of the free ends and the bow is 18 inches, what is the length of the ribbon used? (Each side of the cube is 6 inches). - Rectangular 56801
We are to create a square in the shape of a rectangle with an area of 288 m² (square) so that the sides are whole numbers. What are all the dimensions of the rectangular box we can make? How many is the solution? - Perimeter 16663
The sizes of the sides of a triangle are three natural numbers. The two shorter sides have lengths a = 7 cm and b = 9 cm. What size will the third side be if we want the triangle to have the largest possible perimeter? - The Line segment
Can we construct a line segment if we know: end point and one point inside line
- Paper box
The hard rectangular paper has dimensions of 60 cm and 28 cm. We cut off the corners into equal squares, and the residue was bent to form an open box. How long must the largest volume of the box be beside the squares? - Four-digit 10261
Roman likes magic and math. Last time he conjured three- or four-digit numbers like this: • created two new numbers from the given number by dividing it between digits in the place of hundreds and tens (e.g., from the number 581, he would get 5 and 81), • - Grassland and goat
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is
