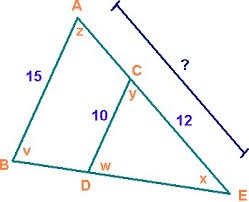
Triangles 6647
For triangles ABC and A'B'C': alpha = alpha with a line, beta with line = beta.
a) are these triangles identical? Why?
b) are these triangles similar? Why?
Result
a) are these triangles identical? Why?
b) are these triangles similar? Why?
Result
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The triangles
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Triangles 6682
Triangles ABC and A'B'C'. They are similar. In triangle ABC, the measures of the two angles are 25 degrees and 65 degrees. Explain why, in triangle A'B'C', the sum of the sizes of the two angles is equal to 90 degrees. - Two angles
The triangles ABC and A'B'C 'are similar. In the ABC triangle, the two angles are 25° and 65°. Explain why in the triangle A'B'C 'is the sum of two angles of 90 degrees. - Triangle - angles
ABC triangle, alpha = 54 degrees 32 minutes, beta = 79 degrees. What are the sizes of the exterior angles?
- One-quarter 13953
Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma. - Intersection 6653
Two straight paths cross, making an angle alpha = 53 degrees 30'. There are two pillars on one of them, one at the intersection, the other at a distance of 500m from it. How far does one have to go from the intersection along the other road to see both po - Similarity coefficient
The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'.
