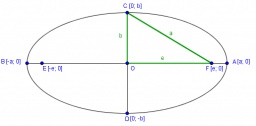
Ellipse

Ellipse is expressed by equation 9x² + 25y² - 54x - 100y - 44 = 0. Find the length of primary and secondary axes, eccentricity, and coordinates of the center of the ellipse.

Correct answer:

o₁ =  10
o₂ =  6
x₀ =  3
y₀ =  2
e =  4

Step-by-step explanation:

$$\begin{gathered} ({\displaystyle \frac{x-x_0}{a}}{)}^2+({\displaystyle \frac{y-y_0}{b}}{)}^2=1 \\ (9x^2-54x)+(25y^2-100y)=44 \\ 9\cdot (x^2-6x)+25(y^2-4y)=44 \\ {x}^2-6x+9=(x-3{)}^2 \\ {y}^2-4y+4=(y-2{)}^2 \\ 9\cdot (x^2-6x+9)+25(y^2-4y+4)=44+9\cdot 9+4\cdot 25 \\ 9\cdot (x-3{)}^2+25\cdot (y-2{)}^2=225 \\ {\displaystyle \frac{9}{225}}\cdot (x-3{)}^2+{\displaystyle \frac{25}{225}}\cdot (y-2{)}^2=1 \\ a=\sqrt{{\displaystyle \frac{225}{9}}}=5 \\ b=\sqrt{{\displaystyle \frac{225}{25}}}=3 \\ {o}_1=2\cdot a=2\cdot 5=10 \end{gathered}$$

$o_2=2\cdot b=2\cdot 3=6$

$x_0=3$

$y_0=2$

$e=\sqrt{a^2-b^2}=\sqrt{5^2-3^2}=4$

Try another example

Related math problems and questions:

• Center
  Calculate the coordinates of the circle center: x² -4x + y² +10y +25 = 0
• Find the 15
  Find the tangent line of the ellipse 9 x² + 16 y² = 144 that has the slope k = -1
• Intersections 3
  Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
• Equation
  Eequation f(x) = 0 has roots x₁ = 64, x₂ = 100, x₃ = 25, x₄ = 49. How many roots have equation f(x²) = 0 ?
• Sphere equation
  Obtain the equation of sphere its centre on the line 3x+2z=0=4x-5y and passes through the points (0,-2,-4) and (2,-1,1).
• Circle
  The circle touches two parallel lines p and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0
• Tangents to ellipse
  Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1].
• Sphere from tree points
  Equation of sphere with three point (a,0,0), (0, a,0), (0,0, a) and center lies on plane x+y+z=a
• Isosceles triangle 9
  Given an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle.
• Circle
  From the equation of a circle: 2x² +2y² +20x -20y +68 = 0 Calculate the coordinates of the center of the circle S[x₀, y₀] and radius of the circle r.
• Prove
  Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
• Find parameters
  Find parameters of the circle in the plane - coordinates of center and radius: ?
• The raw
  The raw data presented here are the scores (out of 100 marks) of a market survey regarding the acceptability of new product launched by a company for random sample of 50 respondents: 40 45 41 45 45 30 30 8 48 25 26 9 23 24 26 29 8 40 41 42 39 35 18 25 35
• Find the 13
  Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3] and C[9, 4].
• Isosceles triangle
  In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C.
• Trapezoid
  trapezoid ABCD a = 35 m, b=28 m c = 11 m and d = 14 m. How to calculate its area?
• On line
  On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0].