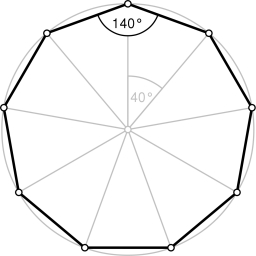
Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm.
Final Answer:
Showing 3 comments:
Math student
I need to draw a nonagon for my daughter and she has to have each at 4cm
5 years ago 1 Like
Matematik
try to start with angle 360/9 = 40°... Draw nine isosceles triangles with base a=4 cm and opposite angle 40°.
Or if you may calculate diameter of described circle - draw a circle and divide it into nine equal segments. (divide by 40° angle)
Or if you may calculate diameter of described circle - draw a circle and divide it into nine equal segments. (divide by 40° angle)
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Nine-gon
Calculate the perimeter of a regular nonagon (9-gon) inscribed in a circle with a radius 18 cm. - Hexagon
Draw a regular hexagon inscribed in a circle with a radius r=15 cm. What is its perimeter? - Calculate 25621
Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm. - Circumscribed 22713
Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm. - Circle and hexagon
Calculate the radius of a circle whose circumference is 8.7 cm longer than the inscribed regular hexagon's circumference. - Calculate 16223
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Decagon
Calculate the area and circumference of the regular decagon when its radius of a circle circumscribing is R = 1m
