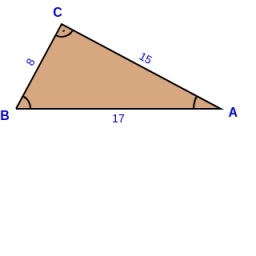
Is right triangle or not
If right triangle ABC, have sides a=13, b=11.5, c=22.5. Find area.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Right triangle
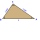A right triangle ABC is given, and c is a hypotenuse. Find the length of the sides a, b, the angle beta if c = 5 and angle alfa = A = 35 degrees. - Right angle
If a, b and c are two sides of a triangle ABC, a right angle in A, find the value on each missing side. If b=10, c=6 - Parallelogram perimeter
The ABC triangle with sides a = 5cm, b = 3cm, c = 40mm has the center of the sides of the K,L,M. How many cm have the KBLM parallelogram perimeter? - Right triangle
Right triangle ABC with side a = 19 and the area S = 95. Calculate the length of the remaining sides. - Euclid 5
Calculate the length of remain sides of a right triangle ABC if a = 7 cm and height vc = 5 cm. - Sin cos tan
In triangle ABC, right-angled at B. Sides/AB/=7cm, /BC/=5cm, /AC/=8.6cm. Find two decimal places. A. Sine C B. Cosine C C. Tangent C. - Right-angled 40961
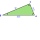A right-angled triangle ABC has sides a = 5 cm, b = 8 cm. The similar triangle A'B'C' is 2.5 times smaller. Calculate what percentage of the area of triangle ABC is the area of triangle A'B'C'. - Triangle
Calculate the triangle's heights ABC if the triangle's sides are a=82, b=44, and c=53. - Triangle and its heights
Calculate the length of the sides of the triangle ABC if va=5 cm, vb=7 cm and side b are 5 cm shorter than side a. - Calculate 3208
Calculate the size of the sides and angles of the triangle ABC, if you know vc = 28, α = 51 ° 19 ', β = 67 ° 38'. - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two interior angles α = 15°28' and β = 45°. - Right-angled 81019
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Angles and sides of the triangle
Triangle ABC has a circumference of 26 cm. Lengths of the sides are as follows: a = 11.2 cm; b = 6.5 cm. Arrange the interior angles in order of their size. ... - Calculate
Calculate the height to the base of the isosceles triangle ABC if the base length is c = 24cm and the arms have a length b = 13cm. - Right triangle trigonometrics
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60°, and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent) - Is right triangle
Find out if the triangle ABC (with right angle at the vertex C) is right if: a) a = 3dm, b = 40cm, c = 0.5m b) a = 8dm, b = 1.2m, c = 6dm - Triangles 2737
The triangles ABC and XYZ are similar. Find the missing lengths of the sides of the triangles. a = 5cm, b = 8cm x = 7.5cm z = 9cm
