Reflector
The circular reflector throws a light cone with a vertex angle 56° and is on 24 m height tower. The axis of the light beam has the axis of the tower angle 11°.
What is the maximum length of the illuminated horizontal plane?
What is the maximum length of the illuminated horizontal plane?
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Tower + pole
On the horizontal plane, there is a vertical tower with a flag pole on its top. At a point 9 m away from the foot if the tower, the angle of elevation of the top and bottom of the flag pole are 60°and 30° respectively. Find the height of the flag pole. - Tower
How many m² of the copper plate should be replaced on the roof of the conical tower shape with a diameter 23 m, and the angle at the axial section's vertex is 119°? - Calculate cone
The rotating cone has a base radius r = 226 mm, and the deviation of the side from the base plane is 56°. Calculate the height of the cone. - Mirror
How far must Paul place a mirror to see the top of the tower 12 m high? The height of Paul's eyes above the horizontal plane is 160 cm, and Paul is from the tower distance of 20 m. - The tower
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands? - Consumption 69174
The tower's roof has the shape of the shell of a rotating cone with a base diameter of 4.3 m. The deviation of the side from the plane of the base is 36°. Calculate the consumption of sheet metal to cover the roof, assuming 8% for waste. - The tower
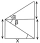From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
