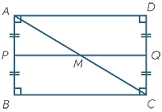
Rectangle JANO
The rectangle has side lengths | JA | = 16cm and | AN | = 12cm. Point S is the center of the JO side, and point T is the center of the JA side. Calculate the perimeter of the pentagon in cm.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Triangle in a square
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Calculate 6885
Triangle with o = 16.8 cm and aspect ratio a:c = 1:2 and b:c = 5:6. Calculate side lengths a =? B =? c =? - Triangle
In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the - Triangle's centroid
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Rectangle and diagonal
In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area. - Rectangle's 81596
The rectangle has a perimeter of 30 cm. The ratio of its sides a: b=2:3. Calculate the sides' lengths and the rectangle's area.
