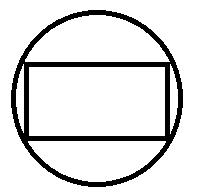
Rectangle and circle

The rectangle ABCD has side lengths a = 40 mm and b = 30 mm and is circumscribed by a circle k. Calculate approximately how many cm is circle long.

Correct result:

x =  157.08 mm

Solution:

x=π⋅ 302+402=157.08 mm

Try another example


We would be pleased if you find an error in the word problem, spelling mistakes, or inaccuracies and send it to us. Thank you!






Showing 0 comments:
avatar




Tips to related online calculators
Do you want to convert length units?
Pythagorean theorem is the base for the right triangle calculator.

You need to know the following knowledge to solve this word math problem:


 
We encourage you to watch this tutorial video on this math problem: video1   video2

Next similar math problems:

  • Tent
    stan Calculate how many liters of air will fit in the tent that has a shield in the shape of an isosceles right triangle with legs r = 3 m long the height = 1.5 m and a side length d = 5 m.
  • Central park in city
    park The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than they walked along the path
  • Rhombus and inscribed circle
    rhombus_2 It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals.
  • Rectangle - parallelogram
    nieco It is given a rectangle that is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD whose vertices are the midpoints of the sides of the rectangle.
  • Garden
    garden_1 Area of a square garden is 6/4 of triangle garden with sides 56 m, 35 m, and 35 m. How many meters of fencing need to fence a square garden?
  • Similarity coefficient
    eqlateral_triangles The ratio of similarity of two equilateral triangles is 3.5 (ie 7:2). The length of the side of smaller triangle is 2.4 cm. Calculate the perimeter and area of ​​the larger triangle.
  • Rhombus ABCD
    rhombus6 Rhombus ABCD, |AC| = 90 cm, |BD| = 49 cm. Calculate the perimeter of the rhombus ABCD.
  • Diagonal
    rectangle_diagonal Calculate the length of the diagonal of the rectangle ABCD with sides a = 8 cm, b = 7 cm.
  • Rectangle - desc circle
    obdelnik_kruh Length of the sides of the rectangle are at a ratio 1: 3 . Radius of the circle circumscribed to rectangle is 10 cm. Calculate the rectangle's perimeter.
  • Canopy
    cone-roof Mr Peter has metal roof cone shape with a height of 127 cm and radius 130 cm over well. He needs paint the roof with anticorrosion. How many kg of color must he buy if the manufacturer specifies the consumption of 1 kg to 3.3 m2?
  • IS trapezoid
    trapezoid_ABCD Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
  • Rectangle
    rectangle_inscribed_circle The rectangle is 21 cm long and 38 cm wide. Determine the radius of the circle circumscribing rectangle.
  • Right trapezoid
    lich_right The right trapezoid has bases 3.2 cm and 62 mm long. The shorter leg has a length 0.25 dm. Calculate the lengths of the diagonals and the second leg.
  • Square circles
    stvorec_kruh Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
  • Area 4gon
    4gon Calculate area of 4-gon, two and the two sides are equal and parallel with lengths 11, 5, 11 and 5. Inner angles are 45°, 135°,45°, 135°.
  • Recursion squares
    squares_reccurent In the square ABCD is inscribed a square so that its vertices lie at the centers of the sides of the square ABCD.The procedure of inscribing square is repeated this way. Side length of square ABCD is a = 22 cm. Calculate: a) the sum of perimeters of all s
  • TV diagonal
    tv_diagonal Diagonal TV is 0.56 m long, how big the television sreen is if the aspect ratio is 16:9?