Gravitation
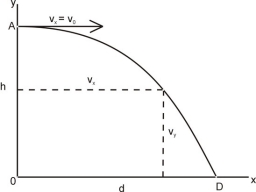
From the top of the 80 m high tower, the body is thrown horizontally with an initial speed of 15 m/s. At what time and at what distance from the foot of the tower does the body hit the horizontal surface of the Earth? (use g = 10 m/s2)
Final Answer:
Tips for related online calculators
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
solid geometryUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Collision of bodies
From point A at a height of 2 m and from point B at a height of 6 m, two bodies are thrown at the same time towards each other. The first from point A with a horizontal speed of 8 m/s, and the second from the direction down at an angle of 45 degrees to th - Projectile height
A 100 g body is ejected vertically upwards from the surface of the Earth at an initial speed of 30 m/s. Determine the height at which the body rises and its potential energy at the path's highest point. - A baseball
A baseball is hit over a fence that is 325 feet away and 110 feet tall. How far did the ball travel in a straight line when it reached the fence? - Fall
The body was thrown vertically upward at speed v0 = 39 m/s. Body height versus time describes equation h = v0 * t - (1)/(2) * 9.8 * t². What is the maximum height of body reach? - Bomber
The aircraft flies at an altitude of 14700 m above the ground at a speed of 619 km/h. At what horizontal distance from point B should be released any body from the aircraft body fall into point B? (g = 9.81 m/s²) - Up and down motion
We throw the body from a height h = 5 m above the Earth vertically upwards v0 = 10 m/s. How long before we let the second body fall freely from the same height to hit the Earth simultaneously? - Bomber
Bomber flies 10 km at 850 km/h. At what horizontal distance from the target must the pilot drop the bomb to hit the target? Don't care about air resistance and consider the gravitational acceleration g=9.81 m/s².
