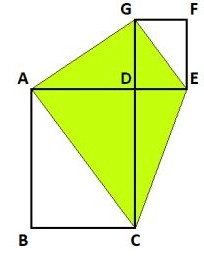
Quadrangle ACEG

The figure shows two rectangles ABCD and DEFG, with |DE|=3 CM, |AD|=6 CM, |DG|= 5, |CD|= 10 CM. Calculate the area of ​​quadrangle ACEG.

Figure description: the rectangles have one vertex D in common. Rectangle ABCD has twice as long sides as DEFG. All sides are either parallel or perpendicular.

Final Answer:

S =  67.5 cm²

Step-by-step explanation:

$$\begin{gathered} a=3\text{cm} \\ A=6\text{cm} \\ b=5\text{cm} \\ B=10\text{cm} \\ {S}_1=\frac{A\cdot B}{2}=\frac{6\cdot 10}{2}=30{\text{cm}}^2 \\ {S}_2=\frac{A\cdot b}{2}=\frac{6\cdot 5}{2}=15{\text{cm}}^2 \\ {S}_3=\frac{a\cdot b}{2}=\frac{3\cdot 5}{2}=\frac{15}{2}=7.5{\text{cm}}^2 \\ {S}_4=\frac{a\cdot B}{2}=\frac{3\cdot 10}{2}=15{\text{cm}}^2 \\ S=S_1+S_2+S_3+S_4=30+15+7.5+15=67.5{\text{cm}}^2 \end{gathered}$$

Try another example