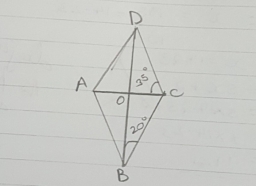
A kite
ABCD is a kite. Angle OBC = 20° and angle OCD = 35°. O is the intersection of diagonals. Find angle ABC, angle ADC, and angle BAD.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Intersection 81594
Given a trapezoid ABCD and the sizes of the interior angles. Angle SDC 32° SAD angle 33° SDA angle 77° Angle CBS 29°, where S is the intersection of the diagonals. What is the size of the angle BSA? - Parallelogram
We know about parallelogram ABCD: length |AB| = 76cm, |BC| = 44cm, and angle ∢BAD = 30°. Find the area of the parallelogram. - Tunnel - quadrilateral
How long will the tunnel AB be, distances AD=35 m, DC=120 m, CB=85 m, and angles ADC=105 degrees and BCD=71 degrees. ABCD is a quadrilateral. - Parallelogram 80761
Construct a parallelogram ABCD if a=5 cm, height to side a is 5 cm, and angle ASB = 120 degrees. S is the intersection of the diagonals. - Parallelogram
Calculate area of the parallelogram ABCD as shown if |AB| = 13 cm, |BC| = 99 cm and angle BAD = 100° - Circumference 16933
In the diamond ABCD, the angle BAD is 60°; the length of the diagonal BD is 7 cm. Calculate the circumference of the diamond. - The intersection of the diagonals
In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle: A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle.
