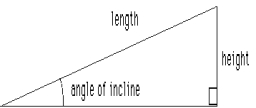
One side
One side is 36 long with a 15° incline. What is the height at the end of that side?
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Parallelogram 62084
OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100 °. What is its area? - Mast shadow
The mast has a 13 m long shadow on a slope rising from the mast foot toward the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Viewing angle
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - The cable car
The cable car is 2610 m long and rises at an angle of 35°. Calculate the height difference between the lower and upper station of the cable car.
- The ladder
The ladder touches a wall at the height of 7.5 m. The angle of the inclination of the ladder is 76°. How far is the lower end of the ladder from the wall? - Balloon and bridge
From the balloon, which is 92 m above the bridge, one end of the bridge is seen at a depth angle of 37° and the second end at a depth angle of 30° 30 '. Calculate the length of the bridge. - Juice box 2
The box with juice has the shape of a cuboid. Internal dimensions are 15 cm, 20 cm, and 32 cm. Suppose the box stays at the smallest base juice level and reaches 4 cm below the upper base. How much internal volume of the box fills juice? How many cm below
