Set of coordinates
Consider the following ordered pairs that represent a relation.
{(–4, –7), (0, 6), (5, –3), (5, 2)}
What can be concluded about the domain and range for this relation?
A. The domain is the y values of the ordered pairs.
B. The range is the set of output values.
C. The given relation is a function.
D. Zero is included in the range of the relation.
E. 5 is included in the domain of this relation.
{(–4, –7), (0, 6), (5, –3), (5, 2)}
What can be concluded about the domain and range for this relation?
A. The domain is the y values of the ordered pairs.
B. The range is the set of output values.
C. The given relation is a function.
D. Zero is included in the range of the relation.
E. 5 is included in the domain of this relation.
Correct answer:
Showing 1 comment:
Math student
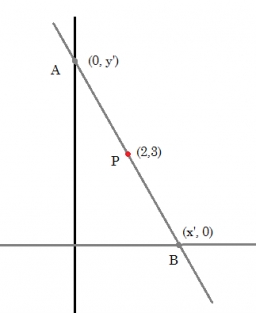
Graph the points (10,7) and (3,8) on the coordinate plane.
Click to graph a point. Click the point again to delete it.
Click to graph a point. Click the point again to delete it.
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Ordered pairs
Given: Set T = {(1,2), (2,3), (3,4), (4,5), (5,5), (6,7), (6,6), (7,8), (8,9), (9,9), (9, 10), (11,12), (12,13), (13,14), (15,16), (16,16), (17,18), (18,19), (20,21)} Find the probability of having an ordered pair wherein the second element is greater tha - Solve 2
Solve integer equation: a +b+c =30 a, b, c = can be an odd natural number from this set (1,3,5,7,9,11,13,15) - Solve
Solve this direct relation by the triplet: 0.25h. .. . . .. .. . . .. .. .. 3 pcs 6.5h. .. . . .. .. . . .. .. . . .. .. x pcs - Equivalent fractions 2
Write the equivalent multiplication expression. 2 1/6÷3/4
- Bivariate data set
Here is a bivariate data set in which you believe y to be the response variable. x y 51.4 44.8 60.2 46.6 60.1 46.8 45.8 46.3 37.4 41.8 72.4 52.5 60 48.2 67.5 49.5 60.9 49.8 51.1 45.7 62.7 49.6 194.9 84.2 Make a scatter plot of this data. Which point is an - Mean
If the mean of the set of data 5, 17, 19, 14, 15, 17, 7, 11, 16, 19, 5, 5, 10, 8, 13, 14, 4, 2, 17, 11, x is -91.74, what is the value of x? - Proportional relationship
The ordered pairs (6,24) and (1, s) represent a proportional relationship. Find the value of s.
