Hexagon
Divide a regular hexagon into lines with nine completely identical parts; none of them must be in a mirror image (you can only rotate individual parts arbitrarily).
Correct answer:
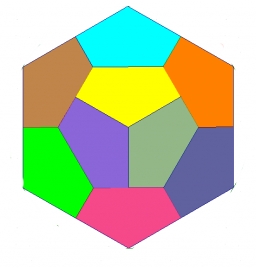
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Individual 6270
Divide three lines with lengths of 12 cm, 24 cm, and 64 cm into equally long and, at the same time, the most extended possible parts. How long will the individual parts be, and how many will there be? - Hexagon = 8 parts
Divide the regular hexagon into eight equal parts. - Collected 38381
The foreman collected 268 kg of apples and must sort them into baskets of 7 kg each. Can they divide the apples correctly? Will all baskets be refilled? How many baskets will they need if they want to put all the apples in the baskets? - Divide
How many different ways can three people divide seven pears and five apples?
- Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Groups
In the 6th class, there are 60 girls and 72 boys. We want to divide them into groups so that the number of girls and boys is the same. How many groups can you create? How many girls will be in the group? - Sons
The father has six sons and ten identical, indistinguishable balls. How many ways can he give the balls to his sons if everyone gets at least one?
