Two rectangles 2
A square area of 36 cm2 is cut out to make two rectangles - A and B. The area's ratio A to B is 2:1. Find the rectangles A and B dimensions.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Check out our ratio calculator.
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- square root
- planimetrics
- area of a shape
- square
- rectangle
- basic functions
- ratio
- reason
- numbers
- fractions
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rectangles 6279
Reduce the dimensions of the rectangle with dimensions of 21 cm and 1.4 dm in a ratio of 4:7. In what proportion will the areas of both rectangles be? - Two rectangles
I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm². What dimensions can this large rectangle have? Write all options. Explain your - Rectangles
Calculate how many squares/rectangles of size 4×3 cm we can cut from a sheet of paper of 36 cm×32 cm. - Right-angled 66364
From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
- Rectangular 81233
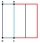A rectangular strip of paper measuring 4 cm x 13 cm is folded as shown. The two resulting rectangles have areas P and Q, where P = 2Q. Calculate the value of x. Note divide the side of 13 cm by x and 13-x. - Three rectangles
Some wire is used to make three rectangles: A, B, and C. Rectangle B's dimensions are 3/5 cm larger than Rectangle A's dimensions, and Rectangle C's dimensions are again 3/5 cm larger than Rectangle B's dimensions. Rectangle A is 2 cm by 3 1/5 cm. What is - The perimeter 3
The perimeter of a rectangle is 35 cm. The length ratio to its width is 3:2. Calculate the rectangle's dimensions.
