Similarity coefficient
The similarity ratio of two equilateral triangles is 4.3 (i.e., 43:10). The length of the side of the smaller triangle is 7.5 cm. Calculate the perimeter and area of the larger triangle.
Final Answer:
Tips for related online calculators
Do you want to convert length units?
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circumference 64104
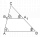 The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '.
The ABC triangle has a circumference of 11 cm. Triangle A'B'C ', similar to triangle ABC, has side lengths of 6 cm, 120 mm, and 1.5 dm larger than triangle ABC. Calculate the area of the triangle A'B'C '. - Centimeters 80859
 Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm².
Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm². - Circumference 42471
 The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm.
The lengths of the sides of the triangle ABC are in the ratio 4:2:5. Calculate the size of the longest side of a similar KLM triangle, whose circumference is 66 cm. - Similarity 80742
 Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm.
Calculate the perimeter of triangle ABC if you know that it is similar to triangle EFG in which e=144 mm, f=164 mm, g=92 mm, and the similarity ratio is 4. Express the result in cm. - Circle section
 An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Triangles
 An equilateral triangle with a side of 16 cm has the same perimeter as an isosceles triangle with an arm of 23 cm. Calculate the base x of an isosceles triangle.
An equilateral triangle with a side of 16 cm has the same perimeter as an isosceles triangle with an arm of 23 cm. Calculate the base x of an isosceles triangle. - Equilateral 6306
 We composed the diamond of four equilateral triangles with a side length of 7 cm. What's his circuit?
We composed the diamond of four equilateral triangles with a side length of 7 cm. What's his circuit?
