Maths practice for 14 year olds - page 157 of 369
Number of problems found: 7369
- Hexagonal pyramid
Find the volume of a regular hexagonal pyramid, the base edge 12 cm long and the side edge 20 cm. - Readers
Readers borrowed 220 books from the library during the first three days. On the second day, readers borrowed half as many books as on the first day and, at the same time, 20 fewer books than on the third day. Depending on the quantity x, express the numbe - Four-component 27131
The four-component ointment contains components A, B, C, and D. Components A and B are mixed in a ratio of 1:2, components B and C in a ratio of 3:5, and components B and D in a ratio of 4:3. In what proportion should the pharmacist mix the ointment? - Pedestrian 27061
Behind a pedestrian walking at an average speed of 5 km/h, a cyclist drove from the same place 3 hours later at an average speed of 20 km/h. How long will it take for a cyclist to catch up with a pedestrian? - Thirty-five 27011
Thirty-five applicants applied for the company's audition. In the first round, they were divided into 3 groups. In the first group, there are 3 people fewer than in the second. In the third, there are 2 more people than in the second. How many candidates - Toothpaste 27001
The father would use the toothpaste alone for 15 days, the mother for 12 days, and the daughter for ten days. It was used by all three for three days, then only the father and mother. How many days have they used it since the beginning of its use? - Calculate 26991
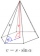How can you calculate the wall height of a pyramid when you know the base edge length is 28 mm and the body height is 42 mm? - Discounting 26971
The original price of the product was 2.55 euros, the price after the discount is 1.99. Find out: a/What % of the original price is the price after the discount b/How much % of the new price is the original price of the product c/o How much % did the prod - Transformation 26961
The output voltage of the transformer is 880 V. The secondary coil has 1200 turns. Determine the voltage to which the primary coil is connected and how many turns it has if a current of 1 A flows through it. The transformation ratio is k = 4. What current - Transformation 26951 The bell uses 8 V alternating voltage obtained from the 220 V mains. The secondary coil of the bell transformer has 60 turns. How many turns must the primary coil have? What is the transformation ratio?
- Coils of transformer
The transformer's primary coil has 1100 turns and is connected to a voltage of 220V. How many turns does the secondary coil have when the voltage is 55 V? Find the transformation ratio and decide what kind of transformation. - Coils of transformer What voltage is generated on the secondary coil of the transformer, which has 1500 turns, if the primary coil is connected to a voltage of 120 V and has 500 turns? What is the transformation ratio, and what kind is the transformation?
- Coils of transformer The primary coil of the transformer has 400 turns. A current of 1.5 A passes through it and is connected to a voltage of 220 V. For the secondary coil, find the voltage, current, and number of turns if the transformation ratio k = 0.1.
- Transformer Transformer - U1 = 230 V, N1 = 300, N2 = 1,200, I1 = 4 A. Calculate the secondary coil's transformation ratio, voltage, and current.
- Candies 26871
Clara mixed a mixture of candies of two types: Ham, ham candies at the price of CZK 210 per 1 kg, and Yum, Yum candies at CZK 150 per 1 kg. She mixed the candies so that the mixture of ham, ham, yum, and yum weighed 10 kg, and the price for 1 kg of the mi - Punishment 26851
Alena, Ivana, Edo, Filip, and Martin came late to school. As a punishment, two will water flowers all over the school after class, and the other three will clean up the classroom. The class teacher couldn't decide who to send to water the flowers, so Juro - Shell area cy
The cylinder's shell area is 300 cm square, and its height is 12 cm. Calculate its volume. - The cylinder
The cylinder's surface area is 300 square meters, and its height is 12 meters. Calculate its volume. - Metal sheets
How much metal sheet is needed to produce eight 4 m long and 12 cm in diameter gutters? During production, joints are calculated at 3% of total consumption. - Which
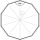Which of the following numbers is the most accurate area of a regular decagon with side s = 2 cm? (A) 9.51 cm² (B) 20 cm² (C) 30.78 cm² (D) 31.84 cm² (E) 32.90 cm2
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
