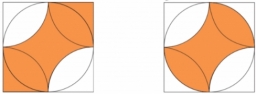
Ratio of squares

A circle is given in which a square is inscribed. The smaller square is inscribed in a circular arc formed by the side of the square and the arc of the circle. What is the ratio of the areas of the large and small squares?

Correct answer:

r =  0:0

Step-by-step explanation:

$$\begin{gathered} r_1=1 \\ u=2r_1=\sqrt{2}{a}_1 \\ {a}_1=2\cdot r_1\mathrm{/}\sqrt{2}=2\cdot 1\mathrm{/}\sqrt{2}=\sqrt{2}\doteq 1.4142 \\ {S}_1=a_1^2=1.4142^2=2 \\ {S}_2=a_2^2=0 \\ r=S_1\mathrm{/}{S}_2=2\mathrm{/}0\approx INF=0:0 \end{gathered}$$

Try another example

Related math problems and questions:

• Arc and segment
  Calculate the length of circular arc l, area of the circular arc S₁ and area of circular segment S₂. Radius of the circle is 11 and corresponding angle is ?.
• Square and circles
  The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
• Circular segment
  Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm and the angle α = 60°. Help formula: S = 1/2 r2. (Β-sinβ)
• Circle arc
  Circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and size of the central angle.
• Circles
  The areas of the two circles are in the ratio 2:20. The larger circle has a diameter 20. Calculate the radius of the smaller circle.
• Infinity
  In a square with side 19 is inscribed circle, the circle is inscribed next square, again circle, and so on to infinity. Calculate the sum of the area of all these squares.
• Squares ratio
  The first square has a side length of a = 6 cm. The second square has a circumference of 6 dm. Calculate the proportions of the perimeters and the proportions of the contents of these squares? (Write the ratio in the basic form). (Perimeter = 4 * a, conte
• Trapezoid - central median
  The central median divides the trapezoid into two smaller trapezoids. Find the ratio of its areas.
• Squares above sides
  Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc
• Silver medal
  To circular silver medal with a diameter of 10 cm is an inscribed gold cross, which consists of five equal squares. What is the content area of the silver part?
• Similarity of squares
  The ratio of the similarity of the squares ABCD and KLMN is 2.5. Square KLMN area is greater than area of a square ABCD with side a: ?
• Quarter circle
  What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
• Circle section
  Equilateral triangle with side 33 is inscribed circle section whose center is in one of the vertices of the triangle and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio betewwn the circumference to the circle sector and
• Three segments
  The circle is divided into 3 segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C?
• MO-Z5-3-66 tiles
  The picture shows a square tiles with side 10 dm which is composed of four identical small rectangles and squares. Circumference of small square is five times smaller than the circumference of the entire tile. Determine the dimensions of the rectangle.
• Ratio of sides
  Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in ratio 2 to 7.
• Folding table
  The folding kitchen table has a rectangular shape with an area of 168dm² (side and is 14 dm long). If necessary, it can be enlarged by sliding two semi-circular plates (at sides b). How much percent will the table area increase? The result round to one-hu