Area of shape - high school - math problems

Number of problems found: 277

  • Pipeline
    pipeline How much percent has changed (reduced) area of pipe cross-section, if circular shape changed to square with same perimeter?
  • Annular area
    medzikrucie2 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
  • Garden
    garden_6 The garden has a rectangular shape and has a circumference of 130 m and area 800.25 m2. Calculate the dimensions of the garden.
  • Interesting property
    rectangles Plot a rectangular shape has the interesting property that circumference in meters and the area in square meters are the same numbers. What are the dimensions of the rectangle?
  • The funnel
    kuzel_rs The funnel has the shape of an equilateral cone. Calculate the content of the area wetted with water if you pour 3 liters of water into the funnel.
  • Airplane
    tu-144 Aviator sees part of the earth's surface with an area of 200,000 square kilometers. How high he flies?
  • The plaster cast
    pyramid_4s The plaster cast has the shape of a regular quadrilateral pyramid. The cover consists of four equilateral triangles with a 5 m side. Calculate its volume and surface area.
  • The farmer
    field_2 The farmer would like to first seed his small field. The required amount depends on the seed area. Field has a triangular shape. The farmer had fenced field, so he knows the lengths of the sides: 119, 111 and 90 meters. Find a suitable way to determine th
  • Inscribed rectangle
    circle_desc_rectangular The circle area is 216. Determine the area of inscribed rectangle with one side 5 long.
  • Quatrefoil
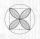    4listek Calculate area of the quatrefoil which is inscribed in a square with side 6 cm.
  • Pentagon
    5gon_3 Calculate the area of a regular pentagon, which diagonal is u=16.
  • Two rectangles 2
    square_2rectangles A square of area 36 cm2 is cut out to make two rectangles. A and B The area of area A to area B is 2 : 1 Find the dimensions of rectangles A and B.
  • Rectangle - area, perimeter
    rectnagles_2 The area of a rectangular field is equal to 300 square meters. Its perimeter is equal to 70 meters. Find the length and width of this rectangle.
  • The roof
    odsek The roof has the shape of a spherical canopy with a base diameter of 8 m and a height of 2 m, calculate the area of the foil with which the roof is covered, when we calculate 13% for waste and residues.
  • Equilateral triangle v2
    eq_triangle Equilateral triangle has a perimeter 36 dm. What is its area?
  • Squaring the Circle
    SquareCircle Calculating side of the square with the same area as the circle of radius 18.
  • Hexagon
    hexagon There is regular hexagon ABCDEF. If area of the triangle ABC is 22, what is area of the hexagon ABCDEF? I do not know how to solve it simply....
  • Rhombus
    rhombus2_3 The rhombus with area 68 has one diagonal is longer by 6 than second one. Calculate the length of the diagonals and rhombus sides.
  • Triangle
    Triangle_trig Calculate the sides of the triangle if its area S = 630 and the second cathethus is shorter by 17.
  • Triangle SSS
    triangle_ABC Calculate perimeter and area of ​​a triangle ABC, if a=53, b=46 and c=40.

Do you have an interesting mathematical word problem that you can't solve it? Submit a math problem, and we can try to solve it.



We will send a solution to your e-mail address. Solved examples are also published here. Please enter the e-mail correctly and check whether you don't have a full mailbox.

Please do not submit problems from current active competitions such as Mathematical Olympiad, correspondence seminars etc...
Examples of area of plane shapes. Examples for secondary school students.