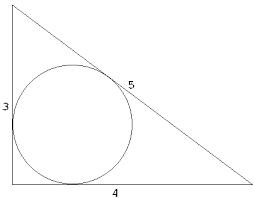
Circle inscribed
Calculate the perimeter and area of a circle inscribed in a triangle measuring 3, 4, and 5 cm.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral 78874
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Triangle
In triangle ABC, there is a point S with the center of the inscribed circle. The area of quadrilateral ABCS is equal to four-fifths of the area of triangle ABC. The lengths of the sides of triangle ABC expressed in centimeters are all integers and the - Inscribed 3689
There is a triangle ABC whose perimeter is 2s (2s = a + b + c), and the circle k (S, ρ) is the inscribed circle of the triangle. Calculate the length of the tangent of the circle k from point A. - Calculate 16223
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle).
- Circumscribed 83152
Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle. - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm. - Circular segment
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
