Volume - math word problems - page 33 of 125
Number of problems found: 2499
- Five-eighth 61644
The glass can hold five-eighth liters of water. How many glasses would we fill with two five-liter bottles? - Percentage 61594
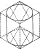Calculate the percentage of the cube volume that represents the volume of the cylinder inscribed in the cube. The cylinder's bases are circles inscribed on two opposite walls of the cube with an edge a = 14 cm. - Prism - right isosceles
Find the volume and surface of a prism with a height of 120 mm. Its base is a right isosceles triangle with a leg length of 5 cm. - Air bubble
The air bubble at the bottom of the lake at a depth of h = 21 m has a radius of r1 = 1 cm at a temperature of t1 = 4°C. The bubble rises slowly to the surface, and its volume increases. Calculate its radius when it reaches the lake's surface, with a tempe - Sphere volume formula
If V=4/3 π r³, find the value of V when r = 7, the value of r when V=113 1/7 - Dividing rod
The 3m long rod should be divided into two parts so that one is 16cm longer than the other. Find the lengths of both parts. - Side wall planes
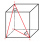Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
- A prism
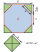A prism with an altitude of 15 cm has a base in the form of a regular octagon inscribed in a square of 10cm x 10cm. Find the volume of the prism. - A box 4
A box open at the top has a rectangular base of 200 mm x 300 mm and an altitude of 150 mm. If the base and the sides are 10 mm thick, find the box's total surface area. - Sphere submerged in the cone
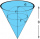A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Block-shaped 60983
The block-shaped aquarium is 40 cm high and has a volume of 80 l. What area in m² will it occupy on the shelf on which it is built? - Dimensions 60943
We will reduce one edge of the block with dimensions of 2cm, 4cm, and 6cm by 20%. How does the volume of a block change? What percentage? - Kindergarten 60933
Each of the 60 kindergarten children drank 1.5 liters of milk on Monday morning and 1.8 liters of milk in the afternoon. How many liters of milk did all the children of this kindergarten drink on Monday? - Hydrogen 60813
One liter of air weighs 1,299 g, and one liter of hydrogen 0.089 8 g. How many times is hydrogen lighter? Round the result to units. - Following 60793 I want to turn to help with the following example. How do I reach an 8% solution? I need to mix 3.5% milk with 33% cream. Thank you for being so helpful.
- Faucets
A large tank is partially filled with a solution. The tank has a faucet that allows the solution to enter the tank at a rate of 16 3/4 liters per minute. The tank also has a drain that allows the solution to leave the tank at a rate of 19 4/5 liters per m - Parallelogram 60483
The area of the parallelogram is 10.24 m2, and its side is 25.6 m. Find the height to this side. - Cylinder 60463
Find the surface and volume of a cylinder whose height is 10 dm and the base circle radius is 20cm. - Corresponding 60311
The drink was mixed from one hundred percent juice and water in a ratio of 1.5 liters of juice to 2.5 liters of water. Calculate how many liters of this drink will be created by mixing 1 liter of water and juice in the corresponding ratio. Calculate how m - The height of prism
A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
Tip: Our volume units converter will help you convert volume units.
