Side wall planes
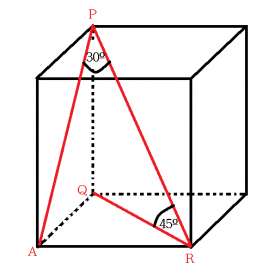
Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Quadrilateral prism
The body diagonal of a regular quadrilateral prism forms an angle of 60° with the base. The edge of the base is 20 cm long. Calculate the volume of the body. - Space diagonal angles
Calculate the angle between the body diagonal and the side edge c of the block with dimensions: a = 28 cm, b = 45 cm, and c = 73 cm. Then, find the angle between the body diagonal and the plane of the base ABCD. - Four sided prism Calculate the volume and surface area of a regular quadrilateral prism whose height is 28.6 cm, and the diagonal body forms a 50-degree angle with the base plane.
- Quadrilateral prism
Calculate the volume (V) and the surface (S) of a regular quadrilateral prism whose height is 28.6 cm and the deviation of the body diagonal from the base plane is 50°. - Trapezoid construction
Construct an isosceles trapezoid, whose base is 6 cm long, the base forms an angle of 30 ° with the diagonal, and the arms are 4 cm long. - Quadrilateral pyramid
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Base diagonal
In a regular four-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the pyramid's surface area and volume.
