Diagonal of Square Problems - page 10 of 18
Number of problems found: 350
- Dig water well
 Mr. Zeman is digging a well. Its diameter is 120 cm, and it plans to be 3.5 meters deep. How long (at least) must be a ladder, after which Mr. Zeman would have eventually come out?
Mr. Zeman is digging a well. Its diameter is 120 cm, and it plans to be 3.5 meters deep. How long (at least) must be a ladder, after which Mr. Zeman would have eventually come out? - Quadrilateral triangle segment
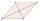 The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Kite
 John a kite, which is diamond-shaped. Its diagonals are 60 cm long and 90 cm long. Calculate: a) the diamond side b) how much paper does John need to make a kite if he needs paper on both sides and needs 5% of the paper for bending?
John a kite, which is diamond-shaped. Its diagonals are 60 cm long and 90 cm long. Calculate: a) the diamond side b) how much paper does John need to make a kite if he needs paper on both sides and needs 5% of the paper for bending? - Rectangle diagonals
 It is given a rectangle with an area of 24 cm² and a circumference of 20 cm. The length of one side is 2 cm larger than the length of the second side. Calculate the length of the diagonal. Length and width are yet expressed in natural numbers.
It is given a rectangle with an area of 24 cm² and a circumference of 20 cm. The length of one side is 2 cm larger than the length of the second side. Calculate the length of the diagonal. Length and width are yet expressed in natural numbers. - Bed 10
 A bed shaped like two equilateral triangles with a common side, with a side length of 2.5 m, is to be planted with seedlings of an ornamental shrub. The gardener recommended leaving 40 cm between the individual seedlings and 10 cm of the perimeter for the
A bed shaped like two equilateral triangles with a common side, with a side length of 2.5 m, is to be planted with seedlings of an ornamental shrub. The gardener recommended leaving 40 cm between the individual seedlings and 10 cm of the perimeter for the - Advertising Board Rent Cost
 Renting a 1m² advertising board costs €780 per month. A rectangular advertising board has a length of 3 m and its diagonal makes an angle of 34 degrees with the longer side. Calculate how much € an entrepreneur will pay for 4 months of renting a blackboar
Renting a 1m² advertising board costs €780 per month. A rectangular advertising board has a length of 3 m and its diagonal makes an angle of 34 degrees with the longer side. Calculate how much € an entrepreneur will pay for 4 months of renting a blackboar - Kite rhombus calculation
 The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend.
The dragon is shaped like a diamond. Its diagonals are 60 cm and 90 cm long. Calculate: a) side of the rhombus b) how much paper do we need to make the kite? If we need to stick it on both sides, it needs 5% of the total area of the paper to bend. - Perpendicular sides
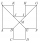 In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ
In the ABCDEFGHIJKL, the two adjacent sides are perpendicular to each other, and all sides except the AL and GF sides are identical. The AL and GF sides are twice as long as the other sides. The lines BG and EL intersect at point M. The quadrilateral ABMJ - Parallelogram diagonal size
 Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals.
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals. - Flowerbed Diagonal Steps Saved
 The rectangular flowerbed has dimensions of 20m and 10m. How many steps will you save if you walk along its diagonal instead of walking along its two sides? Honors with a stride length of 60cm.
The rectangular flowerbed has dimensions of 20m and 10m. How many steps will you save if you walk along its diagonal instead of walking along its two sides? Honors with a stride length of 60cm. - Widescreen monitor
 A wave of widescreen monitors and televisions hit computer businesses. Calculate the area of the LCD monitor with a diagonal size 27 inches at a ratio of 4:3 and then a 16:9 aspect ratio. Is buying widescreen monitors with the same diagonal more advanta
A wave of widescreen monitors and televisions hit computer businesses. Calculate the area of the LCD monitor with a diagonal size 27 inches at a ratio of 4:3 and then a 16:9 aspect ratio. Is buying widescreen monitors with the same diagonal more advanta - Inaccessible direct
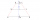 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Central park in city
 The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou
The city park has the shape of a rectangle of 180 meters in length and 120 meters in width. People make their walk through the center of the park from one corner to the second. Calculate how many meters this way is shorter than walking along the path arou - TV diagonal
 A diagonal TV is 0.56 m long. How big is the television screen if the aspect ratio is 16:9?
A diagonal TV is 0.56 m long. How big is the television screen if the aspect ratio is 16:9? - Trapezoid 83
 Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angl
Trapezoid ABCD is composed of five triangles. Points E, and G divide segment AB in the ratio 2:4:3 (in this order) into three segments. Point F is the midpoint of segment AD. Triangle AEF is isosceles and right-angled. Triangles GBC and CDG are right-angl - MO Z9–I–2 - 2017
 VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid.
VO is a longer base in the VODY trapezoid, and the diagonal intersection K divides the VD line in a 3:2 ratio. The area of the KOV triangle is 13.5 cm². Find the area of the entire trapezoid. - Mrak - cloud
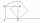 It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s
It is given segment AB, which is 12 cm in length, on which one side of the square MRAK is laid. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB, and point R leaves a paper trail. Draw the whole track of point R until the s - Forces
 Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant?
Forces with magnitudes F1 = 42N and F2 = 35N act at a common point and make an angle of 77°12'. How big is their resultant? - Rectangular trapezoid
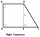 The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters
The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Construct rhombus - MO
 Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all possibilities. How long is a side of a rhombus?
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all possibilities. How long is a side of a rhombus?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
