Equations practice problems - page 102 of 241
Number of problems found: 4814
- The temperature 4
 The temperature was freezing, then doubled, dropped 10 degrees, and increased by 40 degrees. It is now 16 degrees. What was the starting temperature?
The temperature was freezing, then doubled, dropped 10 degrees, and increased by 40 degrees. It is now 16 degrees. What was the starting temperature? - A bucket
 A bucket has 4 liters of water when it is 2/5 full. How much can it hold?
A bucket has 4 liters of water when it is 2/5 full. How much can it hold? - Stone weight puzzle
 The stone weighs 5 kg + half a stone. How much does a stone weigh?
The stone weighs 5 kg + half a stone. How much does a stone weigh? - An equilateral
 An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle?
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Sweets, candy
 Grandfather gave out sweets to four children. At the last moment, two more children came, so to have them all the same, each of the four children would receive four candies less than they would have received if they had not. How much did my grandfather ha
Grandfather gave out sweets to four children. At the last moment, two more children came, so to have them all the same, each of the four children would receive four candies less than they would have received if they had not. How much did my grandfather ha - Hectares of forest
 Twelve workers plant 24 ha of forest in 6 days. How many days will 15 people and 12 people plant in the same area?
Twelve workers plant 24 ha of forest in 6 days. How many days will 15 people and 12 people plant in the same area? - Trapezoid - interior angles
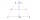 In the trapezoid ABCD (AB II CD) is α = 57°, γ = 4β. Calculate the size of all interior angles.
In the trapezoid ABCD (AB II CD) is α = 57°, γ = 4β. Calculate the size of all interior angles. - Sick colleague
 All the classrooms at school were painted during the holidays. On the first day, 6 painters did one sixth of the required work. From the second day until the painting was finished, only 5 painters worked because one of them got sick. All the painters work
All the classrooms at school were painted during the holidays. On the first day, 6 painters did one sixth of the required work. From the second day until the painting was finished, only 5 painters worked because one of them got sick. All the painters work - Fraction sum puzzle
 The sum of its quarter and its five-twelfths is (-1/3)
The sum of its quarter and its five-twelfths is (-1/3) - Pool filling calculation
 The 300 liters per minute water starts to flow into the empty pool. We will fill the pool in 5 hours. How long would it take to fill a pool with a more powerful 750L pump per minute?
The 300 liters per minute water starts to flow into the empty pool. We will fill the pool in 5 hours. How long would it take to fill a pool with a more powerful 750L pump per minute? - Worker apprentice time
 The trained worker will do the work in 4 hours. The apprentice needs 6 hours for the same work. How many hours and minutes would they do this work if they worked together?
The trained worker will do the work in 4 hours. The apprentice needs 6 hours for the same work. How many hours and minutes would they do this work if they worked together? - The orchard
 Four temporary workers harvested the orchard in 9 days. How many temporary workers do we need for six days?
Four temporary workers harvested the orchard in 9 days. How many temporary workers do we need for six days? - Two groves
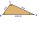 Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'?
Two groves A and B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Salary reduction calculation
 The employer reduced Mr. Mak's salary by 4:5. If he received € 720 in his account, how much did he initially earn?
The employer reduced Mr. Mak's salary by 4:5. If he received € 720 in his account, how much did he initially earn? - Cyclist pedestrian speed
 Cyclist speed and pedestrian speed are in the ratio of 16:3. The pedestrian will drive 4.5 km per hour. How many cyclists will travel in 2 hours?
Cyclist speed and pedestrian speed are in the ratio of 16:3. The pedestrian will drive 4.5 km per hour. How many cyclists will travel in 2 hours? - Linear function
 Write the following problems using x as the unknown variable, using one of the following forms: x+p=q or px=q. Larry ran seven more miles than Barry in a month; if Larry ran 20 miles, how many did Barry run?
Write the following problems using x as the unknown variable, using one of the following forms: x+p=q or px=q. Larry ran seven more miles than Barry in a month; if Larry ran 20 miles, how many did Barry run? - Block volume calculation
 The surface of the block is 558 cm², and its dimensions are in the ratio of 5:3:2. Calculate the volume.
The surface of the block is 558 cm², and its dimensions are in the ratio of 5:3:2. Calculate the volume. - Class student calculation
 About an eighth of the 9th-grade students are interested in studying at the academy, about a sixth at the gymnasium, one quarter at the SOU, one-third at the vocational school, and 3 students at art schools. How many pupils are there in the class?
About an eighth of the 9th-grade students are interested in studying at the academy, about a sixth at the gymnasium, one quarter at the SOU, one-third at the vocational school, and 3 students at art schools. How many pupils are there in the class? - Snail ant meeting
 A snail emerges from the leaf at a speed of 1 cm/min. At the same time, an ant rushes towards it from the stone at a speed of 5 cm/min. The distance between the leaf and the stone is 1.2 meters. How soon will they meet, and at what distance?
A snail emerges from the leaf at a speed of 1 cm/min. At the same time, an ant rushes towards it from the stone at a speed of 5 cm/min. The distance between the leaf and the stone is 1.2 meters. How soon will they meet, and at what distance? - Car meeting calculation
 When and where will the two cars that drove at the same time from cities A and B 90 km apart if the car from city A travels at a speed of 75 km/h and the car from city B at a speed of 60 km/h meet?
When and where will the two cars that drove at the same time from cities A and B 90 km apart if the car from city A travels at a speed of 75 km/h and the car from city B at a speed of 60 km/h meet?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
