Examples for secondary school students - page 42 of 231
Number of problems found: 4611
- Melanie
 Melanie invests a total of $21,500 in two accounts. The first account earned a rate of return of 15% (after a year). However, the second account suffered a 10% loss in the same time period. At the end of one year, the total amount of money gained was $225
Melanie invests a total of $21,500 in two accounts. The first account earned a rate of return of 15% (after a year). However, the second account suffered a 10% loss in the same time period. At the end of one year, the total amount of money gained was $225 - Three flocks
 Flocks of birds pass by, and one bird on a tree asks them, how many of you? And they respond, we are so plenty. The second flock of birds again passes by and asks the bird on a tree, how many of you? The response is we are one-half (1/2) of the first floc
Flocks of birds pass by, and one bird on a tree asks them, how many of you? And they respond, we are so plenty. The second flock of birds again passes by and asks the bird on a tree, how many of you? The response is we are one-half (1/2) of the first floc - Seven segments display
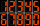 Electronic devices sometimes use the type of digits below, where each digit uses some short stripes. For example, seven uses three small stripes. What is the largest three-digit number that you can make if you use twenty stripes?
Electronic devices sometimes use the type of digits below, where each digit uses some short stripes. For example, seven uses three small stripes. What is the largest three-digit number that you can make if you use twenty stripes? - Busi has
 Busi has a bag containing twenty balls. There are twice as many yellow balls as blue balls, but the yellow balls are only a third of the red balls. The green balls are the same number as the blue balls. How many are each color ball?
Busi has a bag containing twenty balls. There are twice as many yellow balls as blue balls, but the yellow balls are only a third of the red balls. The green balls are the same number as the blue balls. How many are each color ball? - Cryptogram 73784
 Solve the cryptogram (equation with letters, where the letter is one digit) Fot Bal ---- Cvik
Solve the cryptogram (equation with letters, where the letter is one digit) Fot Bal ---- Cvik - Prisoners
 It is estimated that 10% of all federal prisoners have a positive self-image, 40% have a neutral self-image, and the rest have a negative self-image. The estimated probability of rehabilitating a prisoner with a negative self-image is 0.1. With a neutral
It is estimated that 10% of all federal prisoners have a positive self-image, 40% have a neutral self-image, and the rest have a negative self-image. The estimated probability of rehabilitating a prisoner with a negative self-image is 0.1. With a neutral - Triangle 75
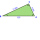 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - Decile
 Find the 5.5th decile of the data: 62, 60, 37, 57, 55, 59, 57, 50, 49, 61
Find the 5.5th decile of the data: 62, 60, 37, 57, 55, 59, 57, 50, 49, 61 - Distribution 73724
 The distribution of the random variable X is given in the following table. Calculate P[X is odd], E[X] and P[1<X≤6] Probability distribution table: xi; 1; 2; 3 ; 4; 5; 6; 7; 8; 9 pi; 0.30; 0.12; 0.18; 0.10; 0.07; 0.07; 0.06; 0.05; 0.05
The distribution of the random variable X is given in the following table. Calculate P[X is odd], E[X] and P[1<X≤6] Probability distribution table: xi; 1; 2; 3 ; 4; 5; 6; 7; 8; 9 pi; 0.30; 0.12; 0.18; 0.10; 0.07; 0.07; 0.06; 0.05; 0.05 - Probability - dice
 I roll six six-sided dice; what is the probability that exactly three threes will fall?
I roll six six-sided dice; what is the probability that exactly three threes will fall? - Menu choice
 In a Jollibee, you have a menu choice of C1, C2, and C3. For dessert, you have a choice of ice cream and mango peach. How many different options do you have?
In a Jollibee, you have a menu choice of C1, C2, and C3. For dessert, you have a choice of ice cream and mango peach. How many different options do you have? - Conditional 73664
 I roll a 7-wall dice. What is the conditional probability that three fell if an odd number fell?
I roll a 7-wall dice. What is the conditional probability that three fell if an odd number fell? - A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an elevation angle of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find the
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an elevation angle of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find the - Maggie
 Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree.
Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree. - Perpendicular 73574
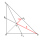 The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line.
The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line. - Sophomores
 There are 3200 students at Lake High School, and 3/8 of these are sophomores. If 3/5 of the sophomores favor the school forming a crew team and 7/10 of the remaining students (not sophomores) are in favor of forming a crew team, how many students are oppo
There are 3200 students at Lake High School, and 3/8 of these are sophomores. If 3/5 of the sophomores favor the school forming a crew team and 7/10 of the remaining students (not sophomores) are in favor of forming a crew team, how many students are oppo - Triangle - BAC angle
 The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much. - Cone - bases
 The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm.
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - A bag 2
 A bag contains seven green and eight red jellybeans. How many ways can five jellybeans be withdrawn from the bag so that the number of green ones withdrawn will be less than 4?
A bag contains seven green and eight red jellybeans. How many ways can five jellybeans be withdrawn from the bag so that the number of green ones withdrawn will be less than 4? - What amount
 What amount of money will be required to repay a loan of $30000 on June 1, 2008? If the loan was made on September 1, 2001, at the interest rate of 14% compounded quarterly.
What amount of money will be required to repay a loan of $30000 on June 1, 2008? If the loan was made on September 1, 2001, at the interest rate of 14% compounded quarterly.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
