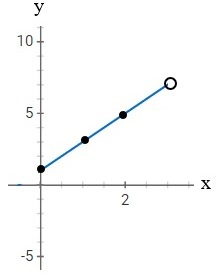
Divide line segment
Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4.
Correct answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Looking for a statistical calculator?
Check out our ratio calculator.
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Looking for a statistical calculator?
Check out our ratio calculator.
You need to know the following knowledge to solve this word math problem:
statisticsgeometryarithmeticbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Points on line segment
Points P and Q belong to segment AB. If AB=a, AP = 2PQ = 2QB, find the distance between point A and the midpoint of segment QB. - Rectangular 3478
A segment AB is drawn in the rectangular coordinate system with endpoints A [1;6] and B [5;2]. The center symmetry is the origin of the coordinate system. Find the coordinates of the center of this segment in this symmetry projection. - Line segment
For the line segment whose endpoints are L[-1, 13] and M[18, 2], find the x and y values for the point located 4 over 7, the distance from L to M. - Three points 2
The three points are A(3, 8), B(6, 2), and C(10, 2). Point D is such that the line DA is perpendicular to AB, and DC is parallel to AB. Calculate the coordinates of D.
- Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - Place vector
Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO. - Number 6911
On the number axis, point P is the image of the number -2.54, and point Q is the image of the number 10.71. Find which number is the point R such that Q is the center of the line PR.
