Koncových 73044
Nájdite bod P na úsečke AB tak, že |AP| = r |AB| . Súradnice koncových bodov: A = (−2, 0, 1), B = (10, 8, 5), pomer r = 1/4.
Správna odpoveď:
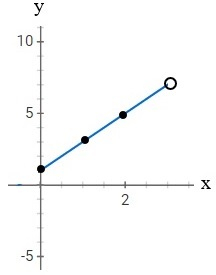
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom aritmetického priemeru?
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Hľadáte štatistickú kalkulačku?
Vyskúšajte našu kalkulačka na prepočet pomeru.
Základom výpočtov v analytickej geometrií je dobrá kalkulačka rovnice priamky, ktorá zo súradníc dvoch bodov v rovine vypočíta smernicový, normálový aj parametrický tvar priamky, smernicu, smerový uhol, smerový vektor, dĺžku úsečky, priesečníky so súradnícovými osami atď.
Hľadáte štatistickú kalkulačku?
Vyskúšajte našu kalkulačka na prepočet pomeru.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Úsečka
Vypočítajte dĺžku úsečky AB, ak súradnice koncových bodov sú A[6, 9] a B[7, -5]. - MO Z9 2019 domáce kolo
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné. Určte pomer obsahov trojuholníkov ABC a PQC. - Na úsečke
Na úsečke AB s dĺžkou 15 cm leží bod C vzdialený od bodu A 4 cm. V akom pomere delí tento bod úsečku AB? - Priesečníkov 74874
Rovnica krivky C je y=2x² - 8x +9 a rovnica priamky L je x + y=3. (1) Nájdite x-ové súradnice priesečníkov L a C. ii) ukázať, že jeden z týchto bodov je tiež - Stred úsečky
Body P & Q patria do úsečky AB. Ak AB = a, AP = 2PQ = 2QB, nájdite vzdialenosť: medzi bodom A a stredom úsečky QB. - Úsečka
Úsečka je daná dvoma bodmi L[-10, -14] a M[-13, -4]. Vypočítajte súradnice bodu na úsečke, ktorý leží v 3/4 vzdialenosti medzi L a M. - Strana uhol, ťažnica,
Mám zostrojiť trojuholník- postup a riešenie a=7cm β= 40 tc=5cm - Smernicový tvar
Nájdite rovnicu priamky prechádzajúcu bodom X [2, 5] a sklonom - smernicou -0,3. Odpoveď zapíšte v tvare y = ax + b, kde a, b sú konštanty. - Vektor PQ
Zo zadaných súradníc bodov P = (5, 8) a Q = (6, 9), nájdite súradnice a veľkosť vektora PQ. - Nájdite 14
Nájdite x v rovnici pomerov: 2:1 4/5=x:3/5 - Daný je 4
Daný je štvorec ABCD. Na jeho uhlopriečke AC leží bod E tak, že platí vzdialenosť AB je rovná vzdialenosti AE. Aká je veľkosť uhla EBC? - Ťažisko
Hmotné body sú rozložené v priestore nasledovne - zadané súradnice v priestore a ich hmotnosti. Nájdite polohu ťažiska tejto sústavy hmotných bodov: A1 [-15; -17; 11] m1 = 80 kg A2 [-16; -13; -5] m2 = 99 kg A - V trojuholníku 15
V trojuholníku ABC určte súradnice bodu B, ak viete, že body A, B ležia na priamke 3x-y-5=0, body A, C ležia na priamke 2x+3y+4=0, bod C leží na súradnicovej osi x a uhol pri vrchole C je pravý. - Kvadratickej 44431
1. V kartézskom rámci o funkciách f a g vieme, že: funkcia (f) je definovaná vzťahom f (x) = 2x2, funkcia (g) je definovaná vzťahom g (x) = x + 3, bod (O) je začiatkom referencie, bod (C) je priesečník grafu funkcie (g ) s osou poradnice, body - MO - trojuholníky
Na stranách AB a AC trojuholníka ABC leží postupne body E a F, na úsečke EF leží bod D. Přmky EF a BC sú rovnobežné a súčasne platí FD:DE = AE:EB = 2:1. Trojuholník ABC má obsah 27 hektárov a úsečkami EF, AD a DB je rozdelený na štyri časti. Určite obsahy - Vektor umiestnite
Vektor AB, ale A(3,-1), B(5,3) umiestnite do bodu C(1,3) tak že, AB=CO - Bod A
Bod A [6 ; -2] . Bod B = [-3 ; 1] Zapíš parametrické vyjadrenie úsečky BA tak, aby t patrilo do uzavretý interval < 0;3 >
