MO Z9 2019 domáce kolo
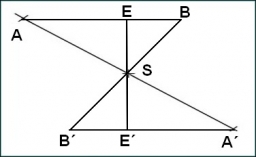
V trojuholníku ABC leží bod P v tretine úsečky AB (bližšie bodu A), bod R je v tretine úsečky PB (bližšie bodu P) a bod Q leží na úsečke BC tak, že uhly PCB a RQB sú zhodné.
Určte pomer obsahov trojuholníkov ABC a PQC.
Určte pomer obsahov trojuholníkov ABC a PQC.
Správna odpoveď:
Zobrazujem 3 komentáre:
Dr Math
no asi tazko, kedze ABC je vacsi trojuholnik ako PQC. PQC lezi v trojuholniku ABC a preto jeho obsah je mensi. preto pomer je 9:2, tj. S(ABC) :S(PQC) = 9:2
5 rokov 2 Likes
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaplanimetriazákladné operácie a pojmytémaÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Z9 – I – 2 MO 2018
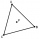V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM. - Pomer obsahov TRN ABC
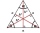V rovnostrannom trojuholníku ABC je bod T jeho ťažiskom, bod R je obrazom bodu T v osovej súmernosti, podľa priamky AB a bod N je obrazom bodu T v osovej súmernosti podľa priamky BC. Určite pomer obsahov trojuholníkov ABC a TRN. - Trojuholník ABC
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Úsečka 6
Úsečka KL má dĺžku 12 cm. Bod X úsečku delí v pomere 1:5. Aká je dĺžka úsečky XL, ak bod X leží bližšie k bodu K? - Na úsečke
Na úsečke AB s dĺžkou 15 cm leží bod C vzdialený od bodu A 4 cm. V akom pomere delí tento bod úsečku AB? - MO - trojuholníky
Na stranách AB a AC trojuholníka ABC leží postupne body E a F, na úsečke EF leží bod D. Přmky EF a BC sú rovnobežné a súčasne platí FD:DE = AE:EB = 2:1. Trojuholník ABC má obsah 27 hektárov a úsečkami EF, AD a DB je rozdelený na štyri časti. Určite obsahy - V trojuholníku 15
V trojuholníku ABC určte súradnice bodu B, ak viete, že body A, B ležia na priamke 3x-y-5=0, body A, C ležia na priamke 2x+3y+4=0, bod C leží na súradnicovej osi x a uhol pri vrchole C je pravý.
