Isolating a variable in the formula - math word problems - page 86 of 145

Number of problems found: 2890

Basket 8054
There were 16 buns in the basket on the table. Josef ate half of it, Eva ate the rest, and Duncho ate it. How much did Dunco eat?
Midpoint 5
FM=3x-4, MG=5x-26, FG=? Point M is the midpoint of FG. Use the given information to find the unknown measure or value.
3rd dimension
The block has a surface of 42 dm², and its dimensions are 3 dm and 2 dm. What is the third dimension?
Dimensions 8044
In the given rectangle, the length is 12 m greater than the width. We get a square if we reduce the length by 10 m and increase the width by 2 m. The area of the original rectangle is 300 m² more than the area of the square. Determine the dimensions of th
Pile of sand
A large pile of sand has been dumped into a conical pile in a warehouse. The slant height of the pile is 20 feet. The diameter of the base of the sandpile is 31 feet. Find the volume of the pile of sand.
Cincinnati
A map is placed on a coordinate grid. Cincinnati is located at (5,4), and San Diego is located at (-10, -3). How far apart is Cincinnati from San Diego on the map? Round to the nearest tenth.
Triangle α and side
Side a in the right triangle has size a = 120 mm, angle α = 60°. How big is the hypotenuse c?
Rectangle 8017
Calculate the other side of the rectangle if one side and the length of the diagonal are known: a = 3cm u = 5cm b =?
The pot
The pot is a cylinder with a volume of V = 7l and an inner diameter of d = 20cm. Find its depth.
Determine 8010
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
Spherical cap
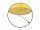Place a part of the sphere on a 4.6 cm cylinder so that the surface of this section is 20 cm². Determine the radius r of the sphere from which we cut the spherical cap.
Inlet minus outlet
Water flows into the tank through two pipes and out of the third pipe spontaneously. Pipe A would fill the tank in 3 hours, pipe B would fill in 4 hours, and pipe C would flow out in 12 hours. If all three pipes open simultaneously, how long will the tank
Equilibrium 7990
At the end of one arm of the equilibrium scales, which are in equilibrium, a lead body with a volume V1 is suspended in the air. At the end of the other arm is an aluminum body with a volume of V2. The balance arms have sizes l1 and l2, lead density h1 =
Contain 7986
The pool is 30 m long, 12 m wide, and 2 m deep. Can it contain 7,000 hl of water? If so, what is the level? If not, how much extra water is there?
The pool - optimization
A block-shaped pool with a volume of 200 m³ is to be built in the recreation area. Its length should be 4 times the width, while the price of 1 m² of the pool bottom is 2 times cheaper than 1 m² of the pool wall. What dimensions must the pool have to make
Entrepreneur 7971
Tatrabanka offers deposits with an annual interest rate of 3.6%. How much EUR must an entrepreneur deposit in Tatrabanka so that at this interest rate, after the end of the year, the bank will credit him with €1,000 interest on the deposit?
Equilateral 7962
After a long dinner, inside a lounge in the shape of a square ABCD, a drunken shopper E lies in such a way that the triangle DEC is equilateral. Spy F lies on the edge of BC, with |EB|=|EF|. What is the size of the angle CEF?
Hyperbola equation
Find the hyperbola equation with the center of S [0; 0], passing through the points: A [5; 3] B [8; -10]
Rectangle
There is a rectangle with a length of 12 cm and a diagonal 8 cm longer than the width. Calculate the area of a rectangle.
Rotating 7947
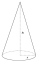In the rotating cone = 100π S rotating cone = 90π v =? r =?

Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.