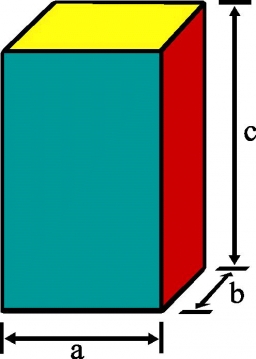
3rd dimension
The block has a surface of 42 dm2, and its dimensions are 3 dm and 2 dm. What is the third dimension?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- solid geometry
- cuboid
- surface area
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Mike chose
Mike chose four identical cubes, three identical prisms, and two identical cylinders from the kit. The edge of the cube is 3 cm long. The prism has two dimensions, the same as the cube. Its third dimension is two times longer. The diameter of the base of - Calculate 6275
A block with edges of lengths of 10 cm and 8 cm has the same volume as a cube with an edge of the length of 1 dm. Calculate the third dimension of the block. Compare the ratio of the surfaces of both bodies. - Cuboid - ratio
Find the volume of a block whose dimensions are in the ratio 2:3:4 and the surface is 117 dm². - Dimensions 7932
The volume of the block is 5760 cm³. For the dimensions of a given block, a: b = 4:3, b: c = 2:5 Calculate its surface.
- Dimension 5079
We will double one block dimension and reduce the other by a third. How does its volume change? - Aquarium
There are 15 liters of water in a block-shaped aquarium with internal dimensions of the bottom of 25 cm and 30 cm. Find the area of water-wetted surfaces. Express the result in dm square. - The pool
The cube-shaped pool has 140 cubic meters of water. Determine the bottom's dimensions if the water's depth is 200 cm and one dimension of the base is 3 m greater than the other. What are the dimensions of the pool bottom?
