Kvádr
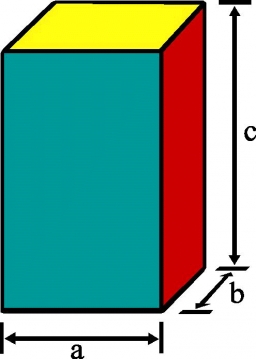
Kvádr má povrch 42 dm2 a jeho rozměry jsou 3 dm a 2 dm. Jaký je třetí rozměr?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Povrch a objem
Vypočítejte povrch a objem kvádru, jehož rozměry jsou 1 m, 50 cm a 6 dm. - Ložný
Ložný prostor nákladního auta má rozměry a = 4,2 m, b = 1,9 m, c = 8,1 dm. Vypočtěte jeho objem. - Objem kvádru
Urči objem kvádru, jehož rozměry jsou v poměru 2:3:4 a povrch je 117 dm². - Kvádr 43
Kvádr o hranách délek 10cm a 8cm má stejný objem jako krychle o hraně délky 1 dm. Vypočítejte třetí rozměr kvádru. Porovnejte poměrem povrchy obou tělěs. - Krabice
Krabice tvaru kvádru má rozměry 30 cm, 25 cm a 40 cm. Načrtni její síť a vypočítej povrch krabice. - Vypočtěte 24
Vypočtěte povrch kvádru s rozměry 54,5 cm, 12,7 cm, 32,3 cm. Výsledek vyjádřete v dm čtverečních. - Pavel 8
Pavel má akvárium tvaru kvádru o objemu 240 litrů. Tomáš má akvárium, jehož všechny rozměry jsou polovina rozměrů Pavlova akvária. Jaký objem má Tomášovo akvárium?
