Line - math word problems - page 17 of 29
Number of problems found: 574
- Construct 10921
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options - Distance between 2 points
Find the distance between the points (7, -9), (-1, -9) - The triangle
Three vertices give the triangle: A [0.0] B [-4.2] C [-6.0] Calculate V (intersection of heights), T (center of gravity), O - the center of a circle circumscribed - Different 9711
A new bus route network was built. There are three stops on each line. In addition, every two lines either do not have a common stop or have only one common stop. What is the largest number of tracks there can be in a town if we know there are only nine d - Identical 8831
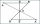In triangle ABC, point P lies closer to point A in the third of line AB, point R is closer to point P in the third of line P, and point Q lies on line BC, so the angles P CB and RQB are identical. Determine the ratio of the area of the triangles ABC and P - Hexagon
Divide a regular hexagon into lines with nine completely identical parts; none of them must be in a mirror image (you can only rotate individual parts arbitrarily). - Set of coordinates Consider the following ordered pairs that represent a relation. {(–4, –7), (0, 6), (5, –3), (5, 2)} What can be concluded about the domain and range for this relation? A. The domain is the y values of the ordered pairs. B. The range is the set of output v
- Eq2 2
Solve the following equation with quadratic members and rational function: (x²+1)/(x-4) + (x²-1)/(x+3) = 23 - ABCDEFGHIJKL 8426
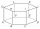The given is a regular hexagonal prism ABCDEFGHIJKL, which has all edges of the same length. Find the degree of the angle formed by the lines BK and CL in degrees. - Belongs 8412
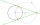Given a circle k(O; 2.5 cm), a line p: /Op/=4 cm, a point T: T belongs to p and at the same time /OT/=4.5 cm. We must find all the circles that will touch the circle k and the line p at point T. - Angle of two lines
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - The railway
The railway line has a gradient of 12 per mille. How many meters will it ascend to a horizontal distance of 4 km? - Perpendicular and parallel
Find the value of t if 2tx+5y-6=0 and 5x-4y+8=0 are perpendicular and parallel lines. What angle does each line make with the x-axis, and find the angle between the lines? - Intersection 8295
Write whether the function is ascending or descending and determine the coordinates of the intersection with the x and y axes: y = 3x-2 y = 5x + 5 y = -0.5x-1 - Divide 8257
Divide a line 9 cm long in a ratio of 3:5:4
- Terminal 8255
Two trams left the station at 9 o'clock. Line 1 goes around the track in 96 minutes. Line 2 returns to the final in 72 minutes. At what time do both teams meet again at the same terminal? - Determine 8133
Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh - Rectangular 8113
The playground has a rectangular shape. The length of the line around its perimeter is 440m. The longer side of the course is 140m long. How many meters does the size of the shorter side of the pitch measure? - Trapezium diagonals
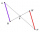It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Together 8086
The first tiler would cover the inside of the pool in 5 working days, and the second would need seven working days for the same work. In how many days would they line the inside of the pool together?
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
