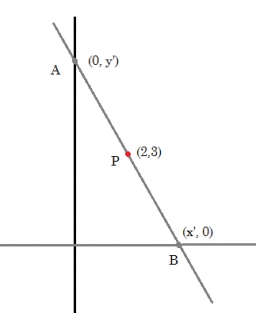
Distance between 2 points
Find the distance between the points (7, -9), (-1, -9)
Final Answer:
Tips for related online calculators
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Construct 8
Construct an analytical geometry problem where it is asked to find the vertices of a triangle ABC: The vertices of this triangle are points A (1,7), B (-5,1) C (5, -11). The said problem should be used the concepts of distance from a point to a line, rati - Points on line segment
Points P and Q belong to segment AB. If AB=a, AP = 2PQ = 2QB, find the distance between point A and the midpoint of segment QB. - RS ABS
Find the distance between points R and S on a number line, with coordinates -4 and -7, respectively. - Add vector
Given that P = (5, 8) and Q = (6, 9), find the component form and magnitude of vector PQ. - On line
On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0]. - Calculate 7214
Two tangents are drawn from point C to a circle with a radius of 76 mm. The distance between the two contact points is 14 mm. Calculate the distance of point C from the center of the circle. - Calculate 6
Calculate the distance of point A[0, 2] from a line passing through points B[9, 5] and C[1, -1].
