Calculate 7214
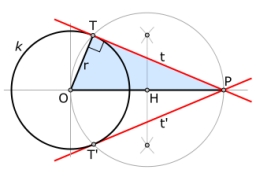
Two tangents are drawn from point C to a circle with a radius of 76 mm. The distance between the two contact points is 14 mm. Calculate the distance of point C from the center of the circle.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryalgebraplanimetricsGrade of the word problem
Related math problems and questions:
- Intersection 83575
Given a circle with a radius r = 4 cm and a point A for which |AS| applies = 10 cm. Calculate the distance of point A from the intersection of the points of contact of the tangents drawn from point A to the circle. - Chord 2
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Tangents
To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center. - Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
- Two chords
Two parallel chords are drawn in a circle with a radius r = 26 cm. One chord has a length of t1 = 48 cm, and the second has a length of t2 = 20 cm, with the center lying between them. Calculate the distance between two chords. - A chord 2
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle. - Connect 6500
Draw the line KL = 55mm. Draw a circle k with center K and a radius of 4cm. Mark the points to belong to the circle and connect them with point L.
