Line - math word problems - page 19 of 29
Number of problems found: 574
- Supplementary angles
One of the supplementary angles is larger by 33° than the second one. Calculate the angles sizes. - Different 6975
Three different bus lines, 80, 81, and 82, depart from the final station at 5h 20min. Line 80 departs every 30 minutes, line 81 every 20 minutes, and line 82 every 40 minutes. What time will they leave again? - Number 6911
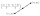On the number axis, point P is the image of the number -2.54, and point Q is the image of the number 10.71. Find which number is the point R such that Q is the center of the line PR. - Rhombus construct
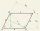Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Difference in temperatures
The temperature in the number line shows minus 15 degrees celsius and 8-degree celsius. What is the difference between the temperatures? - Pieces 6890
Divide the line MN (/ MN / = 9cm) into 11 equal pieces - Air thermal
Imagine that a unit of air rises 3000 meters high. If the temperature decreases 6 degrees Celcius for every 1000 meters, what will be its temperature at 1400 meters, 2000 meters, 2500 meters, and when it reaches the 3000-meter elevation? The starting temp
- Distance of lines
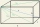Find the distance of lines AE and CG in cuboid ABCDEFGH if given | AB | = 3cm, | AD | = 2 cm, | AE | = 4cm - SSA and geometry
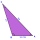The distance between the points P and Q was 356 m measured in the terrain. The viewer can see the PQ line at a 107°22' viewing angle. The observer's distance from P is 271 m. Find the viewing angle of P and the observer. - Equation of the circle
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0 - Two people
Two straight lines cross at right angles. Two people start simultaneously at the point of intersection. John walks at the rate of 4 kph on one road, and Jenelyn walks at the rate of 8 kph on the other road. How long will it take for them to be 20√5 km apa - Right triangle from axes
A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment? - Points collinear
Show that the point A(-1,3), B(3,2), C(11,0) are col-linear. - Tangent 6770
A circle k (S; 2.5 cm) and a point L are given if | SL | = 4cm. Make a tangent to the circle passing through point L. - Two chords
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure.
- __________ 6734
Draw a circle k (S, r = 2cm). Mark the three axes of symmetry of the circle defined by this circle. Each axis of symmetry of the circle passes through __________. - Prove
Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0 - Participants 6671
Out of 86 participants in cycling races, only 56 competitors reached the finish line. How many competitors gave up during the race? - Intersection 6653
Two straight paths cross, making an angle alpha = 53 degrees 30'. There are two pillars on one of them, one at the intersection, the other at a distance of 500m from it. How far does one have to go from the intersection along the other road to see both po - Describe 6648
Images of three numbers are marked on the number line: 0, m, 3m-1. The marked pieces are the same length. a) express the ratio m:(3m-1) b) mark and describe the image of the number 1 on the number line.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
