SSA and geometry
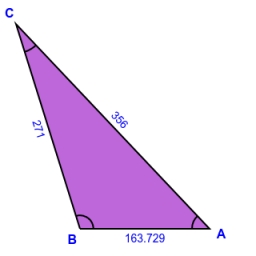
The distance between the points P and Q was 356 m measured in the terrain. The viewer can see the PQ line at a 107°22' viewing angle. The observer's distance from P is 271 m. Find the viewing angle of P and the observer.
Your answer:
Your answer:
Tips for related online calculators
Check out our ratio calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetrybasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Statue
On the pedestal, high 4 m is a statue 2.7 m high. At what distance from the statue must the observer stand to see it at the maximum viewing angle? Distance from the eye of the observer from the ground is 1.7 m. - The pond
We can see the pond at an angle of 65°37'. Its endpoints are 155 m and 177 m away from the observer. What is the width of the pond? - Elevation angle
An airliner currently flying over a location 2,400 m away from the observer's location is seen at an elevation angle of 26° 20'. At what height does the plane fly? - Viewing Two Poles
Two straight paths cross, making an angle alpha = 53 degrees 30'. There are two pillars on one of them, one at the intersection, the other at a distance of 500 m from it. How far does one have to go from the intersection along the other road to see both p - Viewing angle
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - Triangulation - 3 places
Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you. - The chimney
How high is the chimney if we see it from a distance of 60 m at an angle of 42°?
