V terénu - věta SSU
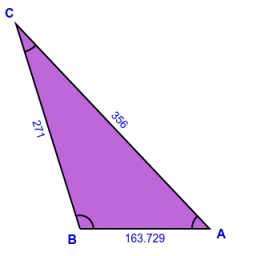
V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriezákladní operace a pojmygoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- SUS a zorný úhel
Rybník vidíme pod zorným úhlem 65° 37'. Jeho kraje jsou vzdáleny 155 m a 177 m od pozorovatele. Jaká je šířka rybníka? - Dopravní 2
Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí? - Pozorovatel 11 Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů.
- Myslivecký posed
Pozorovatel leží na zemi ve vzdálenosti 20 m od mysliveckého posedu vysokého 5 m. A) Pod jakým zorným úhlem vidí posed? B) O kolik se změní zorný úhel, pokud se k posedu přiblíží o 5 m? - Šířka řeky
Ve vzdálenosti 10 m od břehu řeky naměřili základnu AB = 50 m rovnoběžně s břehem. Bod C na druhém břehu řeky je vidět z bodu A pod úhlem 32°30' a z bodu B pod úhlem 42°15'. Vypočítejte šířku řeky. - Pod hloubkovým úhlem
Záchranářský vrtulník je nad místem přistání ve výšce 180 m. Místo záchranné akce je odsud vidět pod hloubkovým úhlem 52°40'. Jak daleko přistane vrtulník od místa záchranářské akce? - Balón
Střed balónu je ve výšce 600 m nad zemí. Ze stanoviště na zemí je střed balónu vidět ve výškovém úhlu o velikosti 38° 20´ a balón je pozorován pod zorným úhlem o velikosti 1° 16´. Vypočítejte průměr balónu.
