Veta SSU geodet
V teréne bola meraná vzdialenosť bodov P a Q rovná 356 m. Úsečka PQ je vidieť od pozorovateľa pod zorným uhlom 107° 22 '. Vzdialenosť pozorovateľa od miesta P je 271 m. Urči zorný uhol, pod ktorým je vidieť miesto P a pozorovateľa.
Vaša odpoveď:
Vaša odpoveď:
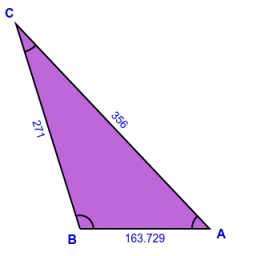
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriazákladné operácie a pojmygoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Výškový uhol
Dopravné lietadlo, ktoré práve prelieta nad miestom 2 400 m vzdialenom od miesta pozorovateľa, je vidieť pod výškovým uhlom o veľkosti 26° 20 '. V akej výške lietadlo letí? - Rybník
Rybník vidíme pod zorným uhlom 65° 37 '. Jeho okraje sú vzdialené 155 m a 177 m od pozorovateľa. Aká je šírka rybníka? - Pozorovateľ - uhly Pozorovateľ vidí lietadlo pod výškovým uhlom 35° (uhol od vodorovnej roviny). V tej chvíli lietadlo hlási výšku 4 km. Ako ďaleko od pozorovateľa je miesto, nad ktorým lietadlo letí. Zaokrúhli na stovky metrov.
- Pozorovateľ 5
Pozorovateľ leží na zemi vo vzdialenosti 20 m od poľovníckeho posedu vysokého 5 m. A) Pod akým zorným uhlom vidí posed? B) O koľko sa zmení zorný uhol, ak sa k posedu priblíži o 5 m? - Teplovzdušný balón
Stred balóna je vo výške 600 m nad zemou. Zo stanovišťa na zemi je stred balóna vidieť vo výškovom uhle o veľkosti 38°20' a balón je pozorovaný pod zorným uhlom o veľkosti 1°16'. Vypočítajte priemer balóna. - Stĺp elektrického vedenia
Z miesta A je vidieť stĺp elektrického vedenia pod uhlom 18 stupňov. Z miesta B, do ktorého sa dostaneme, ideme Ak z Miesta A 30 m smerom od stĺpu pod uhlom 10 stupňov. Urči výšku stĺpa elektrického vedenia. - Výška komína
Zo vzdialenosti 36 metrov od päty komína je vidieť jeho vrch pod uhlom 53 °. Vypočítaj výšku komína. Zaokrúhli na dm.
