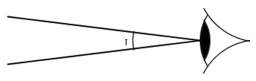
Viewing angle
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- The farmer
The farmer sees the back fence of the land, which is 50 m long at a viewing angle of 30 degrees. It is 92 m away from one end of the fence. How far is it from the other end of the fence? - Observer
The observer sees a straight fence 100 m long in 30° view angle. From one end of the fence is 119 m. How far is it from the other end of the fence? - The angle of view
Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other. - Storm
So far, a storm has traveled 35 miles in 1/2 hour in a direction straight to the observer. If it is 5:00 PM, and the storm is 105 miles away from you, at what time will it reach you? Explain how you solved the problem.
- An angle of depression
The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse? - Horizontal 83362
The observer sees the plane at an elevation angle of 35° (angle from the horizontal plane). At that moment, the plane reported an altitude of 4 km. How far from the observer is the place over which the aircraft flies? They circled for hundreds of meters. - Observer 64354 At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end?
