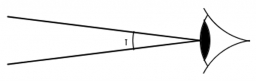
The farmer
The farmer sees the back fence of the land, which is 50 m long at a viewing angle of 30 degrees. It is 92 m away from one end of the fence. How far is it from the other end of the fence?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Viewing angle
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - Observer
The observer sees a straight fence 100 m long in 30° view angle. From one end of the fence is 119 m. How far is it from the other end of the fence? - The angle of view
Determine the angle of view at which the observer sees a rod 16 m long when it is 18 m from one end and 27 m from the other. - The tower
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands?
- Observer 64354
At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end? - A cheetah
A cheetah was separated from his brothers on a hunting mission. The brothers were at the watering hole 120 km away. The lost cheetah knew that he had to make it back before sundown, which was 1.5 hours away. His brothers had planned to leave the wateri - Horizontal 83362
The observer sees the plane at an elevation angle of 35° (angle from the horizontal plane). At that moment, the plane reported an altitude of 4 km. How far from the observer is the place over which the aircraft flies? They circled for hundreds of meters.
