Zorný uhol 2
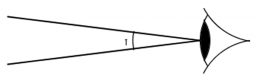
Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m.
Ako ďaleko je pozorovateľ od druhého konca ohrady?
Vaša odpoveď:
Ako ďaleko je pozorovateľ od druhého konca ohrady?
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Hľadáte pomoc s výpočtom koreňov kvadratickej rovnice?
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Máte lineárnu rovnicu alebo sústavu rovníc a hľadáte jej riešenie? Alebo máte kvadratickú rovnicu?
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Kosínusovú vetu priamo používa kalkulačka SUS trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Pozorovateľ
Pozorovateľ vidí priamu ohradu dlhú 60 m v zornom uhle 30°. Od jedného konca ohrady je vzdialený 102 m. Ako ďaleko je od druhého konca ohrady? - Farmar 6
Farmar vidí zadný plot pozemku, ktorý je dlhý 50 m v zornom uhle 30 stupňov. Od jedného konca plota je vzdialený 92 m. Ako ďaleko je od druhého konca plota? - Zorný uhol
Určte veľkosť zorného uhla, pod ktorým vidí pozorovateľ tyč 16 m dlhú, ak je od jedného jej konca vzdialený 18 m a druhého 27 m. - V akom uhle V akom zornom uhle sa javí predmet 70 m dlhý pozorovateľovi, ktorý je od jedného jeho konca vzdialený 50 m a od druhého konca 80 m?
- Pozorovateľ 3
Pozorovateľ vidí vrcholce dvoch stromov v rovnakom uhle α. Od jedného stromu je vzdialený 9 m, od druhého 21 m. Stromy stoja na rovine. Aký vysoký je druhý strom, ak výška prvého je 6 m? Nezabudni, že oči stojaceho človeka sú približne 1,5 m nad zemou. - Hĺbkový uhol
Maják vidí loď pod hĺbkovým uhlom 25°. Pozorovateľ z majáku je vo výške 82 m nad morom. Ako ďaleko je loď od vrchu majáku? - Pozorovateľ - uhly
Pozorovateľ vidí lietadlo pod výškovým uhlom 35° (uhol od vodorovnej roviny). V tej chvíli lietadlo hlási výšku 4 km. Ako ďaleko od pozorovateľa je miesto, nad ktorým lietadlo letí. Zaokrúhli na stovky metrov.
