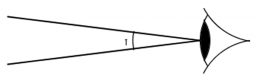
Zorný úhel
Pozorovatel vidí přímou ohradu dlouhou 60 m v zorném úhlu 30°. Od jednoho konce ohrady je vzdálen 102 m.
Jak daleko je pozorovatel od druhého konce ohrady?
Jak daleko je pozorovatel od druhého konce ohrady?
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Pozorovatel
Pozorovatel vidí přímou ohradu dlouhou 100 m v zorném úhlu 30°. Od jedného konce ohrady je vzdálen 170 m. Jak daleko je od druhého konce ohrady? - Farmar
Farmar vidí zadní plot pozemku, který je dlouhý 50 m v zorném úhlu 30 stupňů. Od jednoho konce plotu je vzdálený 92 m. Jak daleko je od druhého konce plotu? - Zorný úhel
Určete velikost zorného úhlu, pod nímž vidí pozorovatel tyč 16 m dlouhou, je-li od jednoho jejího konce vzdálen 18 m a druhého 27 m. - Zorný úhel V jakém zorném úhlu se jeví předmět 70m dlouhý pozorovateli, který je od jednoho jeho konce vzdálen 50m a od druhého konce 80m?
- Hloubkový úhel
Maják vidí loď pod hloubkovým úhlem 25°. Pozorovatel z majáku je ve výšce 82 m nad mořem. Jak daleko je loď od vrchu majáku? - Pozorovatel - vrcholce
Pozorovatel vidí vrcholce dvou stromů ve stejném úhlu α. Od jednoho stromu je vzdálen 9 m, od druhého 21 m. Stromy stojí na rovině. Jak vysoký je druhý strom, pokud výška prvního je 6 m? Nezapomeň, že oči stojícího člověka jsou přibližně 1,5 m nad zemí. - Pozorovatel 11
Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů.
