Line - math word problems - page 24 of 29
Number of problems found: 574
- Diameter 3962
The diameter of the atomic nucleus is 10 to -12cm. How many atoms would fit on a 1 mm line if they could be arranged close together? - Z9-I-4
Kate thought of a five-digit integer. She wrote the sum of this number and its half in the first line of the workbook. Write a total of this number and its fifth on the second line. She wrote a sum of this number and its one nines on the third row. Finall - Coefficient: 3849
Determine the similarity coefficient: a) 4.8; 5.6; 8.4 b) 1.44; 1.68; 2.52 - Hexagon rotation
A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated? - Distance 3575
The distance between the two cities is 25km. This distance was drawn on the map by a line 5 cm long. What is the scale of the map? - Determined 3570
There are 12 points in space, with no three lying on a straight line. How many different planes are determined by these points? - Smokovec 3565
On a tourist map with a scale of 1:20 000, the distance between Starý Smokovec and Nový Smokovec is 24 cm. What is the actual distance?
- Parametric equation
Find the parametric equation of a line with y-intercept (0,-4) and a slope of -2. - Slope
Find the slope of the line: x=t and y=1+t. - Represents 3509
What is the map's scale if the 2.5 cm long line represents 500 km? - Circle tangent
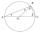It is given to a circle with the center S and a radius of 3.5 cm. The distance from the center to line p is 6 cm. Construct a circle tangent n which is perpendicular to the line p. - Determined 3488
Find out if there is a triangle whose two sides are 5 cm and 8 cm long and the middle bar determined by their centers is 1.5 cm long. - Intervals 3487
The four teams left the terminal together at 5:00 in the morning. Line A runs at 15-minute intervals, line B at 6-minute intervals, line C at 20-minute intervals, and line D at 8-minute intervals. What time did all four lines leave the terminal together a - Rectangular 3478
A segment AB is drawn in the rectangular coordinate system with endpoints A [1;6] and B [5;2]. The center symmetry is the origin of the coordinate system. Find the coordinates of the center of this segment in this symmetry projection. - Parametric equations
Write the parametric equations of height hc in triangle ABC: A = [5; 6], B = [- 2; 4], C = [6; -1]
- Distance of the parallels
Find the distance of the parallels, which equations are: x = 3-4t, y = 2 + t and x = -4t, y = 1 + t (instructions: select a point on one line and find its distance from the other line) - Distance 3245
A map has a scale of 1:55,000. A line of 10 cm shows the distance between places A and B. How long is the distance in reality? - Intersection 3229
Intersection of graphs of functions y = 5x-2 and y = -3x-6 - Numbered
The pages of the book are rectangular with sides 15 cm and 12 cm long. Hansel tore out all the pages and lined them up so that they touched on the shorter side. How long was the line, if you know that the pages were numbered starting from number 1 and the - Right-angled 3147
In a right-angled triangle ABC, the height of side c has a length of 6 cm. The letter D indicates the heel of the height. Line segment AD is 8 cm long. Calculate the area of triangle ABC. ( example on Monitor 9 )
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
