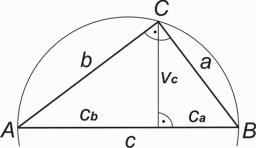
Right triangle area
In a right-angled triangle ABC, the height of side c has a length of 6 cm. The letter D indicates the heel of the height. Line segment AD is 8 cm long. Calculate the area of triangle ABC. ( example on Monitor 9 )
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Squares above sides
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calcu - Rhumbline
Find the circumference and area of the rhumbline ABCD if the short side AD has a length of 5 cm, and the heel of the height from D leading to the AB side divides the AB side into two sections of 3 cm and 4 cm. - Triangle height ratio
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Hypotenuse, euclid
In a right-angled triangle, the hypotenuse has a length of 24 cm. The heel of the height on the hypotenuse divides it into two parts in a ratio of 2:4. What size in cm is the height at the hypotenuse? Calculate the perimeter of this right triangle in cent - Hypotenuse - construct problem A line segment AA1 of length 6 cm is given. Construct all triangles ABC for which AA1 is the hypotenuse, side length BC is 5 cm, and angle gamma is 60°.
- Inequality triangle
The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | < c. - Right-angled triangle
The right-angled triangle XYZ is similar to the triangle ABC, which has a right angle at the vertex X. The following applies: side a = 9 cm, x=4 cm, x = v-4 (v = height of triangle ABC). Calculate the unknown side lengths of both triangles.
