Circle tangent
It is given to a circle with the center S and a radius of 3.5 cm. The distance from the center to line p is 6 cm. Construct a circle tangent n which is perpendicular to the line p.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Touch circle
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides. - Two chords
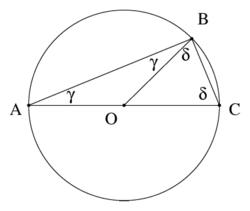
There is a given circle k (center S, radius r). From point A, which lies on circle k, are starting two chords of length r. What angle do chords make? Draw and measure. - Circumscribed iso triangle
Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given.
- Circle chord
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center. - Tangents construct
The circle k is given k (S; 2.5 cm) and an outer line p. Construct a tangent t of the circle that has a line p angle 60°. How many solutions have the task? - Construct rhombus
Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm
