Hexagon rotation
A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated?
Final Answer:
Showing 2 comments:
Deepali.bhavale@gmail.com
Please specify the variables used ...using a figure will be great
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsbasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- The chord
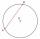 A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°?
A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - Rotatable tower
 The rotatable tower situated in the city center has the ground shape of a regular polygon. If the tower is rotated by 18° around its centerpiece, it looks from the side same. Your task is to calculate at least how many vertices can have a ground plan view
The rotatable tower situated in the city center has the ground shape of a regular polygon. If the tower is rotated by 18° around its centerpiece, it looks from the side same. Your task is to calculate at least how many vertices can have a ground plan view - Angle of diagonal
 The angle between the body diagonal of a regular quadrilateral and its base is 60°. The edge of the base has a length of 10cm. Calculate the body volume.
The angle between the body diagonal of a regular quadrilateral and its base is 60°. The edge of the base has a length of 10cm. Calculate the body volume. - Hexagon area
 The center of the regular hexagon is 21 cm away from its side. Calculate the hexagon side and its area.
The center of the regular hexagon is 21 cm away from its side. Calculate the hexagon side and its area. - Hexagon 8167
 How many dm² of organic glass is needed to produce 50 washers in the shape of a regular hexagon? The side is 8 cm long.
How many dm² of organic glass is needed to produce 50 washers in the shape of a regular hexagon? The side is 8 cm long. - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Hexagonal prism
 The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
