Numbers - math word problems - page 293 of 307
Number of problems found: 6127
- Card sum puzzle
 On the table lay eight cards with the numbers 2,3,5,7,11,13,17,19. Fero chose three cards. He added the numbers written on them and found that their sum was 1 more than the sum of the numbers on the remaining cards. Which cards could have been left on the
On the table lay eight cards with the numbers 2,3,5,7,11,13,17,19. Fero chose three cards. He added the numbers written on them and found that their sum was 1 more than the sum of the numbers on the remaining cards. Which cards could have been left on the - Student row arrangement
 How many ways can we put 19 students in a row when starting a gym?
How many ways can we put 19 students in a row when starting a gym? - Number line arrangement
 Consider the various points corresponding to the numbers a, 2a, 3a + 1 in all possible orders on the straight line representing the number line. For each option, decide whether such an arrangement is possible. If yes, give a specific example; if not, give
Consider the various points corresponding to the numbers a, 2a, 3a + 1 in all possible orders on the straight line representing the number line. For each option, decide whether such an arrangement is possible. If yes, give a specific example; if not, give - Cyclist distance hours
 The cyclist will ride 42.5 km in 2.5 hours. How many kilometers will he cover in 4 hours and 15 minutes?
The cyclist will ride 42.5 km in 2.5 hours. How many kilometers will he cover in 4 hours and 15 minutes? - When will I be a millionaire?
 Barry monthly sends 280 euros to the bank, which he deposits bear interest of 2.1% p. A. Calculate how many months Barry must save to save 1000000 euros. Inflation, interest rate changes, or bank failures are ignored.
Barry monthly sends 280 euros to the bank, which he deposits bear interest of 2.1% p. A. Calculate how many months Barry must save to save 1000000 euros. Inflation, interest rate changes, or bank failures are ignored. - Blueberries
 Five children collect 4 liters of blueberries in 1.5 hours. a) How many minutes do three children take 2 liters of blueberries? b) Eight children will take how many liters of blueberries in 3 hours?
Five children collect 4 liters of blueberries in 1.5 hours. a) How many minutes do three children take 2 liters of blueberries? b) Eight children will take how many liters of blueberries in 3 hours? - Scale of the map
 The distance between the two cities is actually 30 km, and the map is 6 cm. What is the scale of the map?
The distance between the two cities is actually 30 km, and the map is 6 cm. What is the scale of the map? - Compartment ball options
 We have eight compartments where we put three indistinguishable balls and two distinguishable ones. How many options do we have?
We have eight compartments where we put three indistinguishable balls and two distinguishable ones. How many options do we have? - Balls in row
 Calculate the number of ways of placing four black balls, four turquoise balls, and five gold balls in a row.
Calculate the number of ways of placing four black balls, four turquoise balls, and five gold balls in a row. - Four-digit numbers
 The numbers 1,2,3,4,5 are given. Role: a) how many 4-digit numbers can we create if the digits cannot be repeated? b) how many generated numbers will not contain the digit 1? c) How many of the generated numbers will be divisible by 5? d) How many of the
The numbers 1,2,3,4,5 are given. Role: a) how many 4-digit numbers can we create if the digits cannot be repeated? b) how many generated numbers will not contain the digit 1? c) How many of the generated numbers will be divisible by 5? d) How many of the - Sum of inner angles
 Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees.
Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees. - Banknotes
 $ 1390 was collected. How much was in $20 notes, and how many in $50 notes in that order? How many solutions exist?
$ 1390 was collected. How much was in $20 notes, and how many in $50 notes in that order? How many solutions exist? - Acid
 The barrel is 79 liters of 60% acid. How many percent of acids occur when 4 liters are revoked and replaced with the same amount of water?
The barrel is 79 liters of 60% acid. How many percent of acids occur when 4 liters are revoked and replaced with the same amount of water? - Hazard game
 In the Sportka hazard game, six numbers out of 49 are drawn. What is the probability that we will win: a) second prize (we guess five numbers correctly) b) the third prize (we guess four numbers correctly)?
In the Sportka hazard game, six numbers out of 49 are drawn. What is the probability that we will win: a) second prize (we guess five numbers correctly) b) the third prize (we guess four numbers correctly)? - Clock's gears
 In the clock machine, three gears fit together. The largest has 168 teeth, the middle 90 teeth, and the smallest 48 teeth. The middle wheel turns around its axis in 90 seconds. How many times during the day do all the gears meet in the starting position?
In the clock machine, three gears fit together. The largest has 168 teeth, the middle 90 teeth, and the smallest 48 teeth. The middle wheel turns around its axis in 90 seconds. How many times during the day do all the gears meet in the starting position? - Sound triple creation
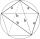 How many triples of sounds can be created from sounds f, o, u, r? You solve using a tree diagram.
How many triples of sounds can be created from sounds f, o, u, r? You solve using a tree diagram. - Book shelf arrangement
 How many ways can we put seven different books on the shelf?
How many ways can we put seven different books on the shelf? - Consecutively numbers
 How many ways are there to arrange the numbers 3, 2, 15, 8, and 6 so that the even numbers are arranged in ascending order (not necessarily consecutively)?
How many ways are there to arrange the numbers 3, 2, 15, 8, and 6 so that the even numbers are arranged in ascending order (not necessarily consecutively)? - Seven segments display
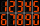 Electronic devices sometimes use the type of digits below, where each digit uses some short stripes. For example, seven uses three small stripes. What is the largest three-digit number that you can make if you use twenty stripes?
Electronic devices sometimes use the type of digits below, where each digit uses some short stripes. For example, seven uses three small stripes. What is the largest three-digit number that you can make if you use twenty stripes? - Zero insertion
 Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then, each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number f
Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then, each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number f
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
